Visualizations that help simplify good EM Engineering
Understanding skin effect and surface currents saves us a lot of time and cost in the design of our product’s shielding and filtering, especially for tough EMC standards such as automotive, military or aerospace. It also helps us to more quickly achieve many other issues in cost-effective EMC design.
This is because visualizing skin effect and surface currents is much easier than trying to visualize what is really going on – the propagation of electromagnetic (EM) waves and fields – and so it more easily provides valuable insights into good EM engineering.
EM engineering includes the disciplines of signal integrity (SI), power integrity (PI) and electromagnetic compatibility (EMC).
Background
My previous article in In Compliance July 2017 – “Introduction to EM Engineering” [1], added to my articles [2] and book [3] on “The Physics of EMC” –
provides the underpinnings for understanding the good EM design techniques that I have been using very successfully since before 1994 (see the testimonials at [4]).
I have been teaching these design techniques in my training courses [5] since 1994, and describing them in UK, US and Chinese EMC magazines since the late 1990s (e.g. [6], [7]) and in my books [8]. It has taken me 47 years to be able to encapsulate this approach in words that any practising electronic, mechanical or PCB designers (and their managers) can understand and easily put into practice immediately.
My approach has always been to communicate exactly what needs to be done, because the plain fact is that modern industry uses such sophisticated semiconductors in such complex products, systems and systems of systems that good EM engineering now needs to be used by every design engineer.
Good EM engineering is no longer an optional added-value item for special projects, it is a fundamental requirement for cost-effectiveness, competitiveness and reliability in the field, regardless of whether any EMC tests are to be applied, or not; and regardless of whether any EMC regulations are to be complied with, or not.
Without using good EM engineering, no electronics company can now expect to be financially successful. And without using good EM engineering, the future world of autonomous robotic cars, aircraft, drones, doctors, surgeons, nurses, care-workers, etc. will simply not happen. (Initial experiences with such complex equipment in the real world – in the real EM environment – would be so poor, that markets will turn against them. It would take at least a decade before public confidence could be built up again to the point where it is now.)
Few electronic, mechanical or PCB designers (or their managers) are taught anything about good EM engineering during their academic schooling, so there is a massive gap between what they need to know for the financial success of their employers, and what they actually do know.
Skin effect is (effectively) a ‘Law of Nature’ – i.e. unavoidable – so if we try to design without respecting it, we will cause difficulties for ourselves (and, more importantly, for our customers and our employers). However, when we understand skin effect and its natural consequences – surface currents – we can more easily visualize what is really going on with the EM waves and fields. This makes it easier to do good EM engineering more quickly, amazing our colleagues, confounding our competitors and leaving us basking warmly in the respect of our peers.
Skin Effect and Surface Currents
DC currents travel through the whole cross-sectional area of a conductor, as sketched in the upper part of Figure 1. But AC currents are forced to flow close to the surface, as shown in the lower part of Figure 1, and this is the skin effect.
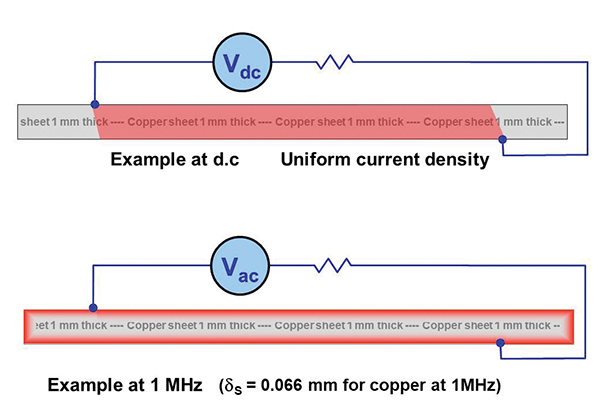
Figure 1: Examples of cross-sectional current density in a 1mm thick copper sheet
Copper at 1 MHz has a skin depth of 66 microns (µm), so we can fit about 15 of them into a 1mm thickness. As I will soon describe, 15 skin depths means a shielding effectiveness of about 130dB (about one ten-millionth), which means that only an extremely small proportion of the 1MHz current flows through the thickness of the 1 mm thick sheet from one side to the other.
Instead, the return currents due to the 1 MHz source have to flow on the surface of the sheet all the way from one circuit terminal to the edges of the sheet, around the edges, and then all the way to the second terminal on the other side of the sheet. Even if the sheet was a mile square!
Electric fields cause displacement currents to flow in all conductor surfaces they impinge upon, and in good conductors these don’t penetrate very far into the depth (the thickness). The effect is to reflect the electric field, and even a kV/m electric field at any frequency from DC to daylight is easily shielded by even a very thin metal foil. At daylight frequencies, we call such a metal foils mirrors.
Magnetic fields cause eddy currents to flow in all conductor surfaces they impinge upon. With a sufficient depth of conductor, these eddy currents generate enough of their own magnetic field, that opposes the impinging field, partly reflecting it away from the conductor. The finite conductivity (non-zero resistivity) of the conductor causes these eddy currents to lose some energy as heat, governing the rate of absorption of the magnetic field as it penetrates the conductor.
How much depth into the conductor is required for good-enough magnetic field shielding depends on the skin depth in that type of conductor. For each skin depth further below the surface of the conductor, the eddy current density diminishes by 1/e, where e is “Eulers number,” approximately 2.71828 [9].
In the EMC world we like to use dB, and 1/e is approximately -8.7 dB, let’s say -9 dB. So we can say that, for each extra skin depth below the surface of a conductor, the density of the eddy currents caused by the impinging magnetic field diminishes by about 9 dB. In other words, our conductor provides magnetic field shielding of 9·k dB, where k is the thickness expressed as the number of skin depths at the frequency of interest.
The formula for calculating skin depth, δS, is:
δS = √(π⋅f⋅μ0⋅μR⋅σ)−1
where:
f is the frequency in Hz
µ0 is the permeability of free space:
4·π·10-7 Henries/meter
µR is the relative permeability of the conductor material, a dimensionless number
σ is its conductivity in Siemens (mho/meter)
This formula can also be expressed in terms of restivity, instead of conductivity, as:
δS = √{ρ/(π·f·μ0·μR)}
where:
ρ is the resistivity of the conductor material in Ω-meters
The above applies to impinging electric and magnetic waves/fields in the near-field, and also to EM waves/fields in the far-field. Chapter 10.1 in [10] provides the academic background for all this, whereas Chapter 15 in [11] provides a more succinct version.
Useful references on skin depth include [12], [13] and [14], and I have sketched a simple graph of some skin depths in Figure 2.
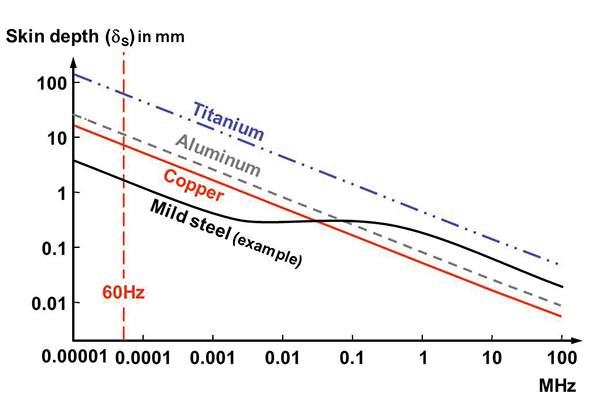
Figure 2: Graph of skin depth for copper, aluminum, titanium and one grade of mild steel
All good non-magnetic conductors (zinc, brass, magnesium, silver, gold, tungsten, etc.) follow pretty much the same lines as copper and aluminum. However, poorer conductors (e.g. tin, bronze, chromium, titanium, Inconel) have larger skin depths at all frequencies.
Any superconductor has zero resistivity (perfect conductivity) and so repels all magnetic fields by pure reflection – its skin depth is zero. This might seem an irrelevance, but some engineers are already working with superconducting materials and there is a lot of research into “room-temperature” (so-called) superconducting materials. Some engineers reading this article will have the opportunity to design with such exotic materials during their careers.
Ferromagnetic conductors such as nickel, iron, steel, etc. have much smaller skin depths below some frequency, due to having a relative permeability (μR) greater than 1. So we see that at, say, 60 Hz, one skin depth in copper is about 8.5 mm, and in aluminum it is about 10.6 mm, but in a particular grade of mild steel (resistivity 10 Ω-meters, relative permeability 200) it reduces to about 1.5 mm. All ferromagnetic materials lose all their relative permeability above some frequency, but in my experience this information is never provided for commodity metals such as mild or stainless steels.
If we were trying to shield the magnetic fields from a 60 Hz transformer, a 3 mm thickness of copper or aluminium could only achieve about -3 dB, but 3 mm of this grade of mild steel could achieve about -18 dB. (There is more to the effective shielding of power-frequency magnetic fields than this, such as the avoidance of magnetic saturation, but this is outside the scope of this article.)
Now here’s the thing:
Conductors still behave as EM shields, no matter what we call them!
All conductors always shield electric, magnetic and EM waves/fields, even if they are used as power, signal or data cables or PCB traces, PCB ground or power planes, or non-electrical brackets, support structures, fixings, etc., etc.
In just the same way, all conductors (wires, cables, PCB traces, brackets, PCB planes, conductive liquids, etc.) still behave as inductors, mismatched transmission lines, and “accidental antennas,” even if we call them “ground” and cover them with green insulation (even if it is green with a yellow stripe!).
(I can’t tell you how much wasted time, effort and cost is caused in the electronics industry every year by technicians, graduate and post-graduate engineers assuming that conductors have different EM characteristics depending on what they are called, or the color of their insulation!)
For example, we see DC conductors with any cross-sectional area, carrying currents of up to hundreds of thousands of amps or more (e.g., for superconducting magnets), but we rarely see 60 Hz power conductors with a copper diameter of more than 20 mm. This is because the skin depth of copper at 60 Hz is about 8.5 mm, so the current density at a greater radial depth than that can be no more than 1/3 of what it is at the surface. Effectively, any round 60 Hz power conductor having a diameter greater than 17 mm is wasting the copper in its centre, adding cost and weight but carrying very little actual current. The metal of the power conductor is shielding itself.
To carry hundreds of thousands of amps at 60 Hz without wasting copper, we use one or more copper busbars, each one no more than about 16 mm thick with sufficient width and number in parallel to handle the current. Or we use as many round conductors in parallel as needed, each of them being no more than 20 mm diameter.
Another example: when designing PCBs, it helps to understand that, above certain frequencies, 0V (“ground”) or power planes carry currents mostly on one side or the other, due to the skin effect. A “½oz” copper layer in a PCB is about 17.5 μm thick, and the skin depth in copper at 100 MHz is about 6.6 μm, so at 100 MHz the currents flowing on one side of the ½oz PCB plane are shielded by about 23 dB from those flowing on the other side. 46 dB for a 1oz copper PCB plane at 100MHz.
This tells us that when a PCB trace that is routed next to one side of the plane changes layers and is routed next to the other side of the same plane, we have to make it possible for the majority of its return currents in the plane to change sides too. As they cannot flow easily through the thickness of the copper plane, because of the shielding created by the skin effect, they have to pour from one side to the other around the edges of the plane. In fact, most of them flow around the edge of the “antipad” – the clearance hole that surrounds the via hole where the trace changed layers – like a miniature Niagara Falls.
Figure 3 sketches something similar. By comparison with the lower part of Figure 1, we see that instead of the surface current having to flow around the edges of the copper sheet, drilling a hole in the sheet allows the plane’s return surface-currents flow in a shorter, hence less inductive, lower overall impedance path.
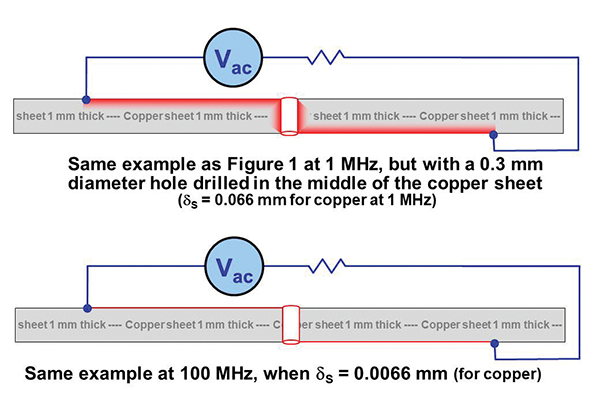
Figure 3: Examples of cross-sectional current densities in 1 mm thick copper sheets that have a small hole drilled in them
Although the hole in the copper sheet allows a shorter overall path length, the current crowding around such a small hole can add significant series inductance. Figure 8 of [1] shows some good examples of current crowding around point contacts. The extra inductance created by the via hole will cause digital waveforms to overshoot and ring, harming their signal integrity (SI) by more than they would if they did not change layers at all. A single via hole can have very important consequences indeed for the SI of very high-speed data signals.
This illustrates another Law of Nature that is very important for good EM Design, that I wrote about in [15]: all currents “prefer” to follow the path(s) of lowest overall impedance (often called loop impedance, because all currents flow in closed loops).
Given a choice of two paths, one having ten times less overall loop impedance than the other, 10/11ths of the current will flow in the lowest impedance path, and 1/11th will flow in the other path.
All AC currents (including strays) flow on the surfaces of conductors, and always flow in the closed loops that have the lowest overall impedance.
At radio frequencies (RF), current cannot flow through any appreciable thickness of a good conductor such as copper or aluminum, a very important real-life effect that is totally ignored by circuit design textbooks and SPICE (and other) circuit simulators. I have seen this lead to fundamental errors in design, for example unnecessarily increasing the size, cost, weight and thermal dissipation of the electronics in military vehicles and platforms, whilst also making it more difficult for them to pass their military EMC tests.
Another issue ignored by circuit simulators is that the higher the frequency, the less an AC current penetrates into the depth (thickness) of a conductor, and this decreases the cross-sectional area of the conductor that is experiencing most of the current. In turn, this increases the resistance in the current path – which can be a big problem for the windings of high-frequency switching power transformers. They often have to be wound with copper tape or Litz wire, instead of the traditional round or square cross-section winding wires, if they are not to be too lossy and run too hot.
Not understanding skin depth and the fact that all AC currents flow as surface currents leads to poor EM engineering, and can lead to very costly mistakes.
Surface Currents and Near-Fields
Quantum electrodynamics (QED) [17] reveals the 1:1 relationship between a conductor’s surface currents and the electric and magnetic near-fields that impinge on that conductor – so we can choose to work either with near-fields or with surface currents.
Many EMC tests are done in the far-field and, for a given 3-dimensional structure, there is a fixed equivalence between its near-fields and its far-fields (although it is not a simple equivalence). So we can see that there is a strong equivalence between a structure’s surface currents and its far-fields.
These strong equivalences mean that by visualizing surface currents we can obtain many very valuable insights into an EM design. For example, when we consider the design of shielding and filtering, we can see that the equivalent of stopping EM fields from leaking in or out (causing immunity or emissions problems respectively) is to design, so that:
All internal surface currents should stay on the inside surfaces of the enclosure, and all external surface currents should stay on the outside surfaces of the enclosure.
I always imagine surface currents to be rather like pouring water onto a product’s enclosure, either on its outside or its inside. If there is a gap, seam or joint that could allow any water to leak from one side of the enclosure to the other, this will also allow electric, magnetic and/or EM waves to leak from one side to the other, degrading the performance of any shielding and/or filtering.
We can extend the water-flow analogy to imagine conductors as being permeable, like cardboard, imagining skin effect as “lower frequency water” soaking through the conductor more than “high frequency water” would. (This might be stretching the analogy a bit far.)
Of course, analogies can only take us so far. For example, water flowing over a surface and leaking out at a seam or joint with another surface will leak out more if the gaps in the seam or joint are bigger. But water has viscosity which means that very narrow gaps will leak less, whereas EM waves have no viscosity so narrow gaps can leak as much as gaps so wide we can put our fingers through them (my famous demonstration [16] shows this very well indeed).
Also, the wavelength of an EM wave/field at a given frequency interacts with gap dimensions, with certain gap dimensions creating resonances that can leak a great deal or very little (discussed in [1]).
Skin Effect and Lossiness
Even if there is no discrete (intentional resistance) in a circuit, there is always some resistance due to the resistivity of its conductors, which is magnified by skin effect as discussed earlier.
For example, a 100 mm length of 2 mm diameter copper conductor with a circular cross-section has a cross-sectional area of about 3 mm2 and a DC resistance of about 0.5 μΩ at normal room temperatures. But it could have a very significant resistance at high frequencies, for example at 1 MHz its skin depth is 66 μm, and the cross-sectional area associated with its first skin depth is about 0.4 mm2, so its end-to-end resistance is about 3 μΩ, representing about a 36-times greater heating effect (power loss) at 1MHz than at DC.
At 100 MHz the cross-sectional area associated with its first skin depth is about 0.04 mm2, so its end-to-end resistance is about 30 μΩ – about 60 times higher than it is at DC and representing about a 3,600-times greater heating effect (power loss) at 100 MHz than at DC.
Where this increased lossiness often has its greatest effect is in resonant circuits. Any resistance makes the resonant frequency lower in value, which can be a nuisance, but the biggest effect is to reduce the quality factor, the Q of the circuit. More resistance means more lossiness means a lower Q value, making it harder to achieve steep filter slopes and narrow bandwidths, especially at microwave frequencies.
Visualizing How Shields Work
Understanding that all non-DC currents flow as surface currents, and that good shielding for EM waves and fields is the same as ensuring that all internal surface currents remain on the inside and all external surface currents remain on the outside, is key to designing shielding.
Water can clearly leak in, or out, through a gap in the box wall, therefore surface currents can too. The more internal surface currents that leak out, the worse the emitted EM fields. The more external surface currents that leak in, the worse the EM immunity.
Visualizing How Shielded Interconnections Actually Work
Visualizing surface currents is the key to quickly and easily dealing with shielded cable connections.
Shielded cables need (what we call) 360° shield coverage along their entire length (i.e., no gaps) to prevent RF leakages, including at all connectors, glands or joints. The skin effect makes RF currents travel on the surfaces of shields, so cable shields should generally be 360° bonded directly to the local RF reference (usually a chassis, PCB 0V plane or enclosure shield) at both ends, to help ensure that internal currents remain flowing on the inside surfaces of the cable’s shielding and external currents remain on its outside surfaces.
We achieve the emissions and immunity specifications by providing optimised return paths (i.e., lowest overall loop impedances) for the flows of the internal surface currents, as Figure 4 shows.
And we do exactly the same for the flows of the external surface currents, also shown on Figure 4.
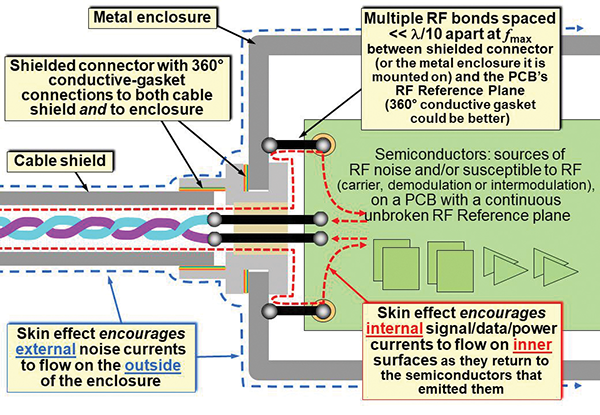
Figure 4: Cable/connector shielding, and the flow of surface currents
Correctly designed and assembled cable shield terminations ensure that enough of the internal surface currents remain flowing on the inside (i.e., enough of the internal fields remain inside) to meet the emissions specification. This also helps ensure that enough of the external surface currents remain flowing on the outside (i.e., enough of the external fields remain outside) to meet the immunity specification.
It is hard to visualize EM waves and fields, but – as Figure 4 shows – it is easy to visualize surface currents, which makes them a big help in doing good EM engineering.
Figure 5 shows a practical implementation of Figure 4, in a desktop PC from 2002.

Figure 5: An example of a cost-effective implementation of Figure 4
Figure 6 shows some examples of the types of die-cut flexible EMC gaskets used for connector panels such as the one shown in Figure 5.
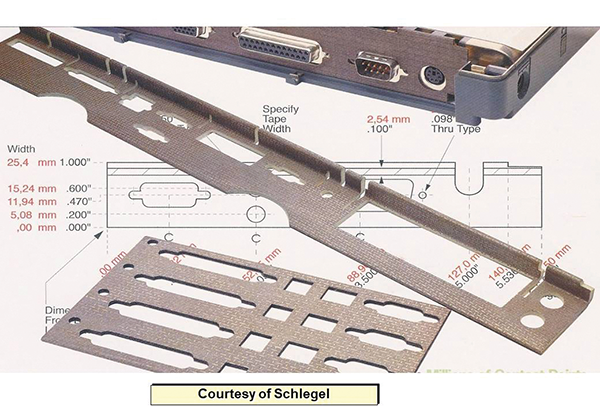
Figure 6: Examples of die-cut flexible EMC gaskets for connector panels, as used in Figure 5
Way back in the 1970s the rule in the professional audio industry was that cable shields were always pigtailed, and indeed the standard pro-audio cable connector (known as the XLR) dedicated its Pin 1 to these pigtails.
Visualizing the paths taken by the surface currents immediately reveals that the pigtailed shield connection allows internal surface currents to flow on the outside of the cable shield and product enclosure shield. And it also allows external surface currents to flow on the inside of the cable shield and product enclosure shield.
Clearly, a pigtailed cable shield connection cannot provide good shielding effectiveness, and we don’t need to research and understand the massive amount of academic and testing work that has been done over the last 30 or more years to prove this very point. We can see it instantly, merely by visualizing surface currents and applying the simple “internal surface currents must flow inside, external surface currents must flow outside” guideline.
The issue of how to achieve good pro-audio (or instrumentation) performance at the frequencies where the cable shield material isn’t thick enough to provide enough skin depths for keeping internal and external currents well-segregated is dealt with in [18]. This has special relevance for the commonplace worries about so-called “ground loops” or “hum loops” in systems and installations.
If there is no metal chassis or enclosure that can be used as an overall product shield, it is possible to achieve the same benefits by appropriate PCB design/layout, using low-cost board-level shielding (BLS) where high levels of shielding are required, as described in detail in [19]. However, given the fast pace of change in the electronics industry, any textbook (other than the most academic) is out of date within a year or two of publication, so I provide continually-updated details in my training courses [20] and [21].
Visualizing How Filtered Interconnections Actually Work
The “filtering effectiveness” of a conductor filter’s performance depends upon the impedance of its RF reference plane (usually a PCB’s 0V/GND plane, or the product’s chassis or enclosure shield). It also depends on the impedance of the filter’s bonding method to that reference plane.
The above paragraph says everything we need to know but provides no practical guidance. For example, we might understand it to mean that a single bonding point between filter and reference plane would be perfect, as long as we make the resistance of the bonding point less than a few μΩ. But that assumption would be wrong, because even if a single filter bond had a negligible resistance, its impedance (Z) is actually Z = R + (j·2·π·f·L) – 1/(j·2·π·f·C), that is, it depends on the bond’s inductance and capacitance, as well as on its resistance. Although the inductance associated with a single filter bonding point is significant, it is quite difficult to visualize.
Also, the electric and magnetic near-fields on one side of a filter have stray couplings from one side to the other, which depend totally on the physical structure of the filter and its surrounding conductors and insulators.
Circuit simulators such as SPICE assume that all currents and voltages remain inside conductors – which is never true – they are really propagating magnetic and electric waves (i.e. near-fields) in the spaces around the conductors. Such over-simplification is one of the main reasons why filter circuit simulations always predict better “filtering effectiveness” than the filters achieve in real life, especially when trying to achieve more than 40 dB attenuation at frequencies above 100 MHz.
So, we have lots of good advice about how to assemble/install filters so that they will function as well as required, but none of it gives us any practical guidance.
However, visualizing the surface currents is the key to quickly and easily dealing with the design of filter assembly/installation.
For the best EMC performance, a filter’s assembly/installation should allow both the internal and external surface currents to naturally flow in their optimum paths (i.e. the ones with the lowest overall loop impedance)
Correctly designed and assembled filter assembly/installation helps ensure that a sufficiently small amount of the internal surface current leaks to the outside, to meet the emissions specification. It also helps ensure that a sufficiently small amount of the external surface current leaks to the inside, to meet the immunity specification.
Thus, by visualizing surface currents flowing like sheets of water, we easily design so that little-enough of the internal fields leak to the outside, for low-enough RF emissions. And that little-enough of the external fields leak to the inside, for good-enough RF immunity.
It is hard to visualize (and design with) EM waves and fields, but – as Figure 7 shows – it is easy to visualize (and design with) surface currents.
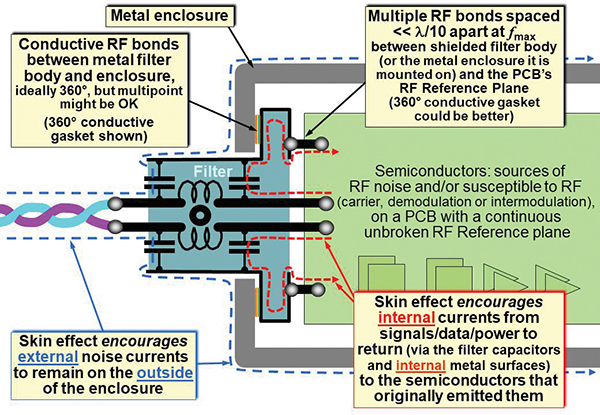
Figure 7: Filter assembly/installation, and the flow of surface currents
The filter schematic shown in Figure 7 is simple for the purposes of making a visual point. There is a wide variety of filter schematics, many of which are more complex than the simple π-filter sketched. Higher-performance filters often use feedthrough capacitors or, better still, feedthrough tee and π “filter pins” (e.g., as used in very costly high-specification military filtered connectors).
Figure 7 shows an example of a chassis-mounted signal, data or power filter for ease of showing visualization of the surface currents. The same principles apply to filters assembled onto PCBs, with capacitors soldered to the continuous unbroken RF reference plane, usually the 0V (or “GND”) plane.
It is equally practicable to achieve good filter performance with PCB-mounted filters, especially when using BLS, and the necessary techniques are described in [19] and updated in [20] and [[21]. Achieving the high-performance required for the toughest military EMC test specifications with PCB-mounted filters and no overall metal enclosure is still beyond us (but we are working on it.)
Where PCB-mounted filters are used in products that rely on an overall enclosure shield, it is very important indeed for the PCB’s reference plane to make a very low impedance RF bond to the metal enclosure. This will generally be easiest to achieve by using a shielded connector, like those shown in Figure 5, even where the filtered cables themselves are not shielded.
As before – the statement of bond impedance in the previous paragraph provides little practical design guidance. And also as before – visualizing the internal/external surface currents and ensuring that they remain inside/outside the overall enclosure makes good design easy.
An Overview of Shielding and Filtering
Figure 8 shows a sketch from one of my training courses concerning the achievement of successful shielding and filtering. Note the very strong admonishments to RF-bond any/every cable shield or other conductor (whether they are electrical conductors or not) to the shielded enclosure’s surface at the point of the conductor’s entry or exit.
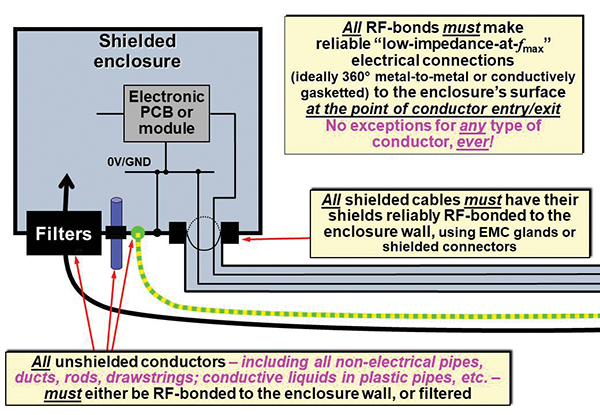
Figure 8: Overview: dealing with conductors that enter/exit a shielded enclosure
The reasons for this are entirely understandable when we visualize keeping all of the external currents on the outside of the enclosure, and all the internal surface currents on its inside.
And when we are faced with a product that uses a shielded overall enclosure but is not complying with its required EMC tests, we can assess it by visualizing all of the possible routes where surface currents might leak to the wrong side.
Of course, we can quickly find the leaky points by using close-field probes, but they can’t show us how to fix the problem and the solution might not be obvious. However, visualizing all of the possible ways by which surface currents can leak in or out at the leaky points is a very powerful way of quickly determining how best to fix the EMC test failure.
Finally, Figure 9 shows a practical example of the type of EMC design problem that for some reason I came across a lot in 2017.

Figure 9: An example of a military-grade shielded enclosure with a leak
I think the annotations on Figure 9 are so clear that I don’t need to repeat them here, but I would like to make a final point:
Filters cannot provide good “filtering effectiveness” on their own
Filter manufacturers never print assembly/installation disclaimers or warnings on their datasheets; or show how their filters were actually tested or describe how their filters should be assembled/installed in order to achieve something approaching their datasheet specifications.
So it is understandable that designers will assume that filter assembly/installation is irrelevant, that they will assume that filters will achieve their full specifications all on their own. I often meet designers who have made this erroneous assumption, when I am EMC fault-finding.
In fact, filter datasheet specifications are only valid when the filters are correctly installed in the wall of a well-shielded enclosure. This is how their manufacturers test them, and this is how they must be used in real-life products in order to stand any chance of achieving their datasheet specifications!
A designer who understands skin effect and surface currents and applies this knowledge in the very simple easy and quick ways I have described in this article could never make the mistake of assuming that a filter could achieve its full datasheet performance without being properly integrated with appropriate shielding. Understanding skin effect and surface currents and applying this as described in this article is also a powerful tool for avoiding many other causes of EMC problems, not just incorrect filter assembly or installation.
Conclusions
Understanding skin effect well-enough to visualize the flows of surface currents as proxies for near-fields is a very powerful technique in good EM engineering (i.e., quick, cost-effective SI, PI and EMC design) and fault-finding. I hope this brief introduction will stimulate readers to find out more, and to start to use this very effective technique.
References
- “Introduction to EM Engineering”, Keith Armstrong, pages 20-37 in the July 2017 Edition of In Compliance, https://incompliancemag.com/DigEd/icm1707
- “The Physics of EMC”, Keith Armstrong, a series of articles originally published in The EMC Journal in 2009 and 2010, free download from www.emcstandards.co.uk/the-physical-basis-of-emc
- “The Physics of EMC”, Keith Armstrong, Nutwood UK October 2010, ISBN: 978-0-9555118-3-7, full color graphics throughout, printed to order: https://emc-eandt.com/index.php/emc-books/
- www.emcstandards.co.uk/testimonials
- www.emcstandards.co.uk/online-training
- www.compliance-club.com/keitharmstrong.aspx
- SAFETY & EMC Magazine, visit www.semc.cesi.cn/gqmle.asp and search by <<Armstrong>> for articles published in Chinese (mostly), and some in English
- See all Armstrong’s textbooks at https://emc-eandt.com/index.php/emc-books
- https://en.wikipedia.org/wiki/E_(mathematical_constant)
- “Introduction to Electromagnetic Compatibility, 2nd Edition”, Clayton R Paul, Wiley-Interscience, January 2006, ISBN: 978-0-471-75500-5
- “EMC for Product Designers, 5th Edition”, Tim Williams, Newnes, 2016, Paperback ISBN: 9780081010167, eBook ISBN: 9780081010143, www.bh.com/newnes
- Skin depth material properties: www.rfcafe.com/references/electrical/cond-high-freq.htm
- Skin depth formula: www.rfcafe.com/references/electrical/skin-depth.htm
- Skin depth on-line calculator: www.rfcafe.com/references/calculators/skin-depth-calculator.htm
- “Cost-effective EMC Design by Working with the Laws of Physics”, Keith Armstrong, from www.emcstandards.co.uk/additional-resources1
- “Cherry Clough’s EMC Demonstration”, www.cherryclough.com/userfiles/file/W800%20emissions%20demo.doc
- “QED, the Strange Theory of Light and Matter”, Richard P. Feynman, Princeton University Press, Paperback (2014) ISBN: 9780691164090, E-book ISBN: 9781400847464
- “Designing I/Os so they will not suffer from ‘ground loop’ currents in cable screens (shields)”, Keith Armstrong, free download:
www.emcstandards.co.uk/designing-ios-so-they-will-not-suffer-from-g - “EMC for Printed Circuit Boards – Basic and Advanced Design and Layout Techniques, Edition 2”, Keith Armstrong, Nutwood UK December 2010, ISBN 978-0-9555118-5-1, full color graphics throughout, printed to order: https://emc-eandt.com/index.php/emc-books
- “Essential PCB design/layout techniques for cost-effective SI, PI and EMC in 2018”, www.emcstandards.co.uk/essential-pcb-designlayout-techniques-for-cost
- “Advanced PCB design techniques for cost-effective SI, PI and EMC in 2018”, www.emcstandards.co.uk/advanced-pcb-design-for-cost-effective-si-pi-an
