Choosing the Right Magnetic Materials to Filter EMI
Solutions to electromagnetic interference (EMI) problems can be complex in many cases. But when you come back from the lab with unsuccessful radiated emission results, it can be frustrating to hear, “Didn’t you try adding a ferrite?” When used wisely in a good design, ferrites can work very well, but there is a reason they are sometimes called “prayer beads” – we throw them on cables and pray they work.
Let us start with the basics, highly simplified. Common passive components are resistors, capacitors, and inductors. One simple way to differentiate them is that in a resistor, both the current and voltage can change instantaneously. However, in a capacitor, voltage cannot change instantaneously. And in an inductor, current cannot change instantaneously.
All three of these aspects (resistance, capacitance, and inductance) are present in any conductor. Conductive materials, in our case wires, are not perfect metals and have resistance. They have a capacitance to other conductors based on the area each conductor has and their separation. And when carrying a current, they have inductance due to the magnetic field generated by the current in the wire. Knowing that each of these three characteristics exists and cannot be eliminated can be used to the advantage of the circuit design. If we must live with inductance, we might as well wisely put it to use.
The amount of inductance in a wire can be increased by making loops in the wires through which the current can flow. Coiling the wire has the effect of concentrating the magnetic field, or flux, through the middle of the coil, and inducing some back electromotive force on the opposite side of the coil.
To increase this effect, a magnetic material having a permeability greater than 1 is placed inside the coil. If the material is ring-shaped, a toroid, and the wire is wrapped around this core material, the inductance can significantly increase, and the residual and uncontrolled magnetic fields reduced. Being able to control these magnetic fields is important since these fields can create currents in other conductors. If those conductors are sensitive circuits with minimal currents in them, having uncontrolled magnetic fields can induce unwanted signals, which is a source of susceptibility.
Choosing the Materials to Use
One aspect of magnetic materials that makes them desirable is permeability. To explain permeability using simple terms, permeability can be thought of as the ease of the material to conduct magnetic fields. The higher the permeability, the easier it is for magnetic fields to flow through it. This is not how much total field or flux it can contain. A copper wire may be more conductive than an iron wire. But if it is too small a gauge, it will not be able to handle as much current. So if the core is too small, even if it has a high permeability, it can only contain so much magnetic field before it becomes saturated.
This factor becomes an important parameter for inductors and ferrites that might have an initial amount of current flowing in the wire. If the equipment operates with a current of 4 amperes DC, the inductor or ferrite on the power line will see a continuous magnetic field based on that current. If you have an inductor rated for 5 amperes maximum current with the given number of turns wound on the core, you may find the core has limitations on how well it will perform. The issue is that the rating may be based on when the material begins to be saturated and cannot handle additional field.
Figure 1 depicts a figure commonly known as a B-H curve.1 The horizontal axis represents the magnetic field strength induced on the core, which is based on the number of turns on the core and the current in the wire. The axis may also be called a magnetizing force. The vertical axis represents the resulting magnetic field density induced inside the material, or flux density. The areas at the top and bottom of the curve where the curve begins to flatten out represent the point at which the material begins to saturate and lose its ability to handle any more magnetic flux. This is due to the internal crystalline structure containing the magnetic dipoles all being aligned by the induced magnetic field. Once the dipoles all are aligned, the core is saturated and no additional magnetization is available from the material.
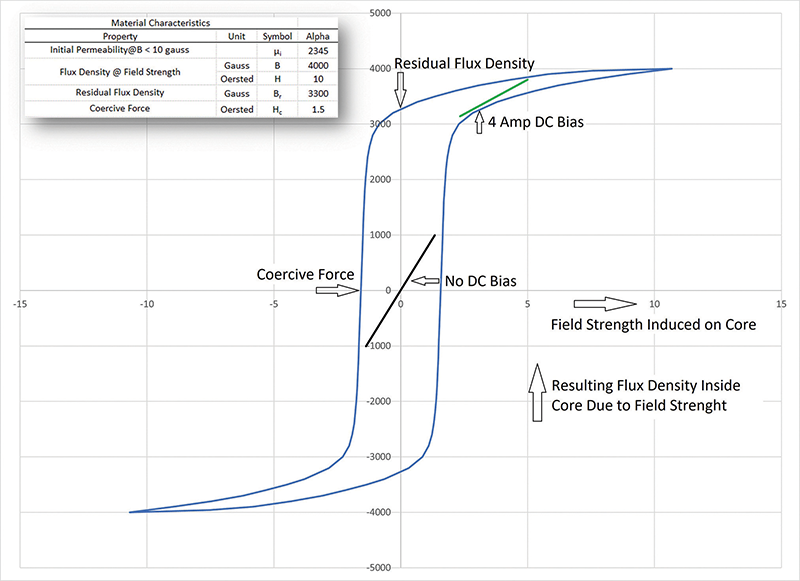
The black diagonal line represents the area in which the core will operate if no DC bias is induced on the core. Notice that the line is more vertical than the green line above and a bit to the right. The green line is the area where the core operates if a DC current is induced on the core. Notice that the green line is less vertical than the black line. For the same change in the field strength inside the core, the change in flux is 2000 Gauss for the black line and only 500 Gauss for the green line. If the DC bias is increased, the induced flux continues to decrease.
Figure 1 illustrates the reduction in the effectiveness of the core due to the bias current. The more current and resulting field strength on the core, the more the core will lose its ability to operate as an inductor. Though shown as simple lines, the actual curves for these two lines would have an open-eye shape similar to the B-H curve, and the green line will flatten with a higher induced magnetic field.
Remember that a core that is wound as a common mode inductor will have both the line current to the load and the return current wound in the same direction, but with the current flowing in opposite directions. The result is the total line current through the core will be zero or near zero. As a result, the core will be operating near the center of the B-H curve (the area of the black line), and the effectiveness of the material maximized for common mode currents. Common mode currents will flow in the same direction through the core, and thus experience a much higher impedance than the differential current. This is what makes common mode inductors so effective.
For this curve, there are two more important parameters to understand. First is at the top, the residual flux density, also called remanence. This is the flux density that remains in the material if the core is driven to saturation, in this case, +10 Oersted or more. If the current returns to 0 amperes, the core is magnetized, which is the remanence of the core. To demagnetize the core, will require a negative field strength and thus a current in the opposite direction. The required field strength to demagnetize the core back to zero Gauss is called the coercive force, or the coercivity of the material, and is shown on the horizontal axis to the left of the curve.
The term “soft ferrites” refers to these last two parameters. The lower the remanence of the core, and the lower the coercive force needed to demagnetize the core, the softer the ferrite. For permanent magnets, this B-H curve can become very wide and in some cases have very sharp corners, making the curve look block-shaped. The softer the ferrite, the more it turns into a lazy S shape, with lower residual flux density. Toroids made from powdered iron will have very low residual flux compared to saturation. In comparison, hard ferrites or hard magnetic materials can be used as a permanent magnet. Once driven to saturation, the remanence of the material is what creates the magnet.
These values become important in the performance of the inductor. When harder core materials are used, the result is greater losses in the core. Also, if the core is too conductive, eddy currents can be created inside the core, and both can result in inefficiencies and excessive heating. So, for use in switching power supplies and the like, the choice of core materials becomes very important, which is why powdered iron and soft ferrites are used. Note that, up to a point, ferrites will maintain their inductance with increasing current in the core better than powdered iron. Once saturation occurs, ferrites radically lose their inductive characteristics, whereas powdered iron degrades much more gradually but continues to be useful.
Molypermalloy powder cores, known as MPP, have been used for decades because of their higher permeability over powdered iron, along with very low core losses and other positive characteristics. However, with higher-speed switching power supplies, MPP cores can have a frequency limitation and may not be the best choice. For this reason, ferrite cores are being considered for highest-speed switch mode power supplies.
Ferrites are typically composed of manganese and zinc or nickel and zinc, mixed with iron. Manganese-zinc ferrites will have higher permeability than nickel-zinc but will have a limited frequency range. In general, the lower the permeability of a material, the higher the frequency range in which it will work. This should be carefully noted when choosing a ferrite as an EMI filter. If there is a radiated emissions issue above 100 MHz, a nickel-zinc core will be the best choice for a filter. And there are other aspects to consider when choosing these cores. Magnesium zinc ferrites are now being developed that have similar characteristics in high frequency material but avoid the use of nickel.
In Figure 2, a ferrite’s permeability is plotted over the frequency range.2 As is common with ferrite manufacturers, two lines are given for the permeability: 1) µ’ representing the real or initial permeability, and 2) µ’’ for the imaginary or lossy component of the core. For the lower frequency manganese-zinc cores, the initial permeability µ’ is higher, but may drop more quickly and be ineffective as an inductor above a few megahertz. However, the lossy aspect of the core might provide benefits at higher frequencies. The range where µ’’ becomes significant is a loss range and can be thought of as resistive but not inductive. Since it is not an inductive component in this frequency range, it is not useful as a transformer or purely as an inductor. When plotted on an impedance analyzer capable of showing phase angle, the inductive portion will appear at 90 degrees (voltage leading current), while the phase of the µ’’ portion will be near 0 degrees.
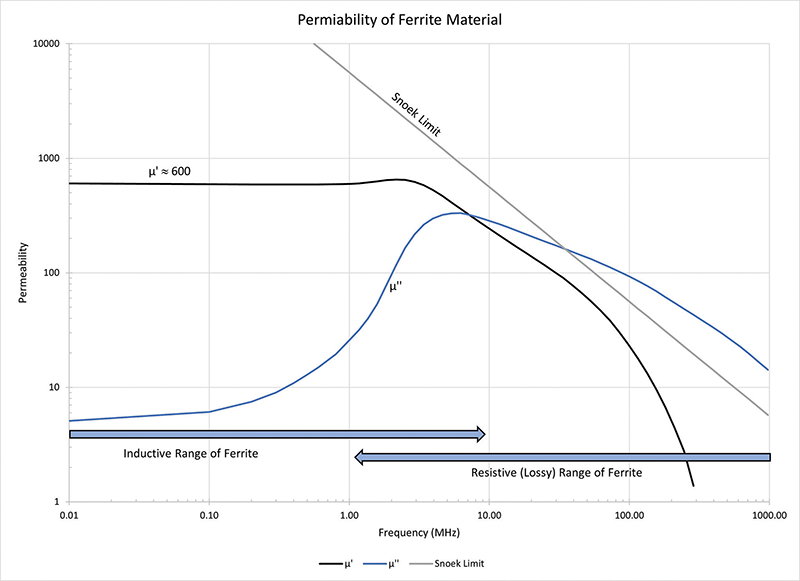
A material of this nature may be useful as a power transformer in the flat region of the permeability, µ,’ about 1 MHz in this case. In this region, the loss factors are still low. As an inductor, a higher frequency can be used, up to the point where µ’ starts to roll off but before the loss factor µ’’ becomes dominant, about 5 MHz. Above this range, the material may be best used as a suppression device, where the loss factor µ’’ dominates but has not rolled off too much, about 100 MHz.
Notice the line called the Snoek Limit, also known as Snoek’s Law. Dr. Jacob L. Snoek found these characteristics in ferrites in his research published in 1947. The general limit for ferrites is simplified as a line with the formula 5600/(frequency in MHz). Plots depicting the real permeabilities of ferrites with this limit show that the µ’ line may approach this limit but does not cross it. The loss factors tend to cross the limit but with little margin. With this in mind, ferrites that have high permeability at high frequency do not exist at this time. Materials that exceed the Snoek Limit are being created but are not commercially available to our knowledge.
How to Choose
The following questions address the key aspects that should be considered when choosing a core for EMI purposes.
Where is the core being used? Power lines or signal line? Internal or external to the unit? Inductors by nature create magnetic fields. The fields are not completely captured in the core material and some “leakage inductance” will exist. If the type of core used is gapped, such as an E core, bobbin, or other types of structures, the fact there are two or more pieces to the core means that some type of gap exists. Gaps will bloom uncontrolled magnetic fields.
All these magnetic fields can cross-coupled into other electronics and cause cross-coupled energy to be generated in other wires, circuits, or structures. Each of these can be the cause of emissions or susceptibility.
If the filter is mounted in the chassis wall of the equipment or located outside of the chassis, and assuming the chassis is a solid metal, the control of these fields becomes less critical due to the location of the filter.
Note that most signal lines will have much lower currents than power lines. When this is the case, the size and nature of the inductor used also changes. Ferrites used as common mode inductors may be beneficial on signal lines to assure the intended differential signals remain differential and do not “leak” a return current by some uncontrolled path. These uncontrolled returns are often the source of radiated emissions.
Will it be a power line filter, common mode filter, transformer, or other use?
If an inductor is needed and the core is placed on individual current carrying lines, the use of ferrites may be less desirable. This is because the current can saturate the material. If the core is placed on an AC power line and does go into saturation at the peak of the current, the core will be driven in and out of saturation two times each cycle (120 times a second on a 60 Hz line). This effect has been seen to create emissions more than decrease them.
Thus, choosing the right material for differential mode power line inductors is important. Powdered iron, MPP, and other such materials are designed to handle these types of currents in a more controlled manner.
Common mode filters using ferrites work best when the sum of all currents in all wires passing through the core is zero or very close to zero. In the case where the power and power return lines are not balanced and a return path may exist in other signal lines, which can occur in some DC equipment configurations, the imbalance can limit the effectiveness of the core.
What frequency range will the material need to operate?
When very high-frequency materials are needed, ferrites are often the best material to consider, especially those containing nickel or magnesium. Most manganese materials may work well up to a few megahertz but have limited use above that. Very high permeability materials tend not to have high-frequency effectiveness.
This can often be noticed in the value of permeability. If the material has a permeability of less than about 1500 or 2000, the likelihood is that the material will work well at high frequencies. If the permeability is over 5000, it likely will not work.
How much impedance will be needed?
Remember that most inductors and common mode chokes will have a maximum impedance typically less than 1-5 kΩ or so. If you need 10 kΩ or more to have adequate impedance to a signal, inductors alone may not be helpful. In these cases, a small amount of capacitance, if it can be used, may provide more benefit than a great deal of inductance.
Remember that creating high values of inductance will often require many turns on a core. Having a large number of turns will have two effects. First, there may be a chance of saturation of the core, as stated earlier. Second, the number of windings on the core will begin to become increasingly capacitive with each other. This leakage capacitance will reduce the high-frequency effectiveness of the core. The capacitance effectively bypasses the inductors from input to output. Impedance graphs of inductors with many windings will increase to some maximum before dropping when the leakage capacitance becomes dominant.
Summary
Not all inductors are created equal. It is important to know how these materials work, the frequency range within which they work, and what benefits can be obtained from their use. Know when to use differential mode inductors and what materials will be best to use for the current demand on that line. Location, core structure, number of windings, and many other aspects are all important factors to consider in choosing the magnetic to use.
Bibliography
- Harris, V. G. (2022). Modern Ferrites, Volume 2: Emerging Technologies and Applications. Wiley.
- Kaiser, K. L. (2005). Electromagnetic Compatibility Handbook. CRC Press.
- Paul, D. C. (2006). Introduction to Electromagnetic Compatibility, Second Edition. Wiley Interscience.
- Snoek, D. J. (1947). New Developments In Ferromagnetic Materials. Elsevier Publishing Company.
- Brander, T.; Gerfer, A.; Rall, B.; Zenkner, H. (2010). Trilogy of Magnetics. Wurth Elektronik.
- Burket, C. (2010). All Ferrite Beads Are Not Created Equal – Understanding the Importance of Ferrite Bead Material Behavior. TDK website
- Parker, C. U. (2011). Using Ferrites to Suppress EMI. Fair-Rite Corporation
- With additional information from:
Endnotes
- This curve and material characteristics are invented by the author, and no commercially available material is known to have these properties. The curve is based on actual ferrite materials and similar performance might be expected of such a material.
- As with the B-H curve, these characteristics are adapted from real materials, and though similar, these values are not from a commercially available product.
