This article uses a classical circuit-theory model of a series RLC circuit to explain the phenomenon of ringing on a transmission line, or a PCB trace (see [1] for the transmission line-theory model of ringing).
Fundamental Background
A typical series RLC circuit configuration is shown in Figure 1.
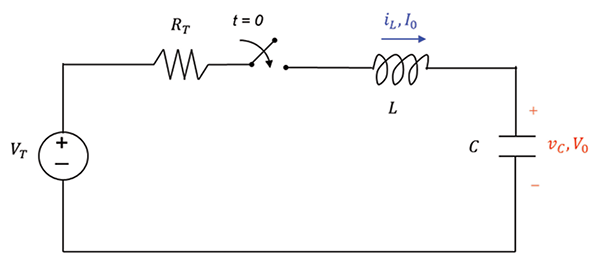
At the t = 0 switch closes and a dc voltage source, VT, is connected to a series LC configuration. In general, the capacitor has an initial voltage of V0 and the inductor has an initial current of I0.
This circuit is governed by the differential equation [2].
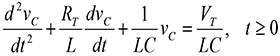 (1)
(1)
or using the damping ratio, ζ, and undamped natural frequency, ω0,
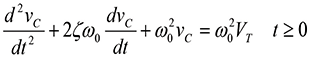 (2)
(2)
where
![]() (3a)
(3a)
![]() (3b)
(3b)
The type of the circuit’s response depends on the value of the damping ratio, ζ. When 0 < ζ < 1, the response is underdamped and has the form
![]() (4)
(4)
where ωd, called damped natural frequency is given by
![]() (5)
(5)
and the constants K and θ are evaluated using the initial conditions V0 and I0.
Many practical pulse circuits can be represented by the lumped equivalent circuit shown in Figure 2.
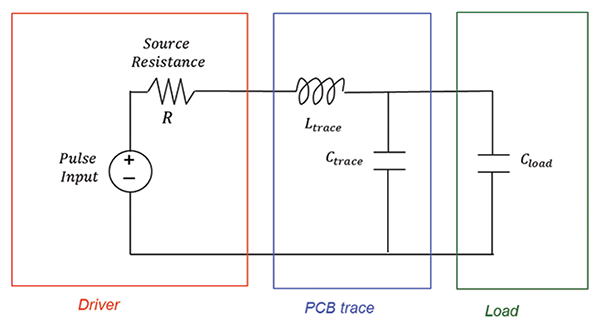
When ringing occurs the voltage across the capacitors exhibits sinusoidal oscillations; i.e., the circuit is underdamped.
Solving Eq. (3a) for ζ we obtain
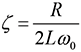 (6)
(6)
Substituting for ω0 from Eq. (3b) into Eq. (6) results in
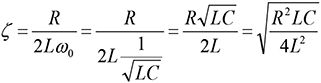 (7)
(7)
Or
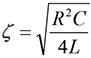 (8)
(8)
To avoid ringing we need ζ ≥ 1, or equivalently
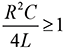 (9)
(9)
In Eq. (9) L and C represent the total loop inductance and the total shunt capacitance, respectively. Thus, in order to avoid ringing the loop inductance would have to satisfy the following inequality
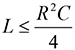 (10)
(10)
Let’s use some typical values for R and C and let R = 20Ω,
C = 10pF. Then the loop inductance would have to satisfy
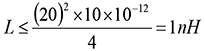 (11)
(11)
The total circuit loop inductance in any practical electronic circuit exceeds this value and gives rise to the phenomenon of ringing.
Ringing Measurements
The laboratory test set-up to measure ringing is shown in Figure 3.

The circuit diagram showing all intentional circuit components is shown in Figure 4.
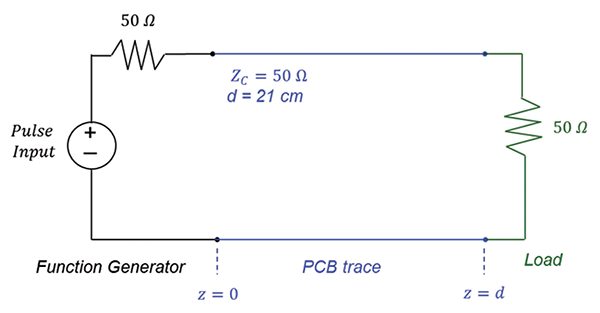
The function generator produces a 1 MHz trapezoidal 1Vpp pulse train with the adjustable rise and fall time. With the rise and fall times set to 10 ns, the voltage measured at the input to the PCB trace is shown in Figure 5.
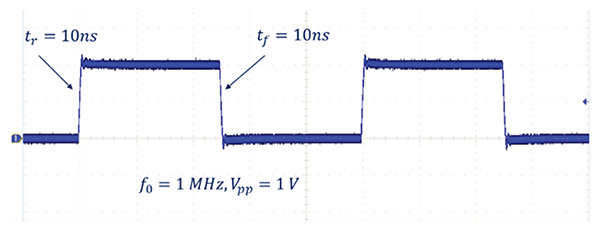
There is no noticeable ringing present at the input to the trace.
Figure 6(a) shows the waveform when the rise time has been changed to 2.5 ns while the fall time stayed at 10 ns. In Figure 6(b) both the rise time and fall time are at 2.5 ns.
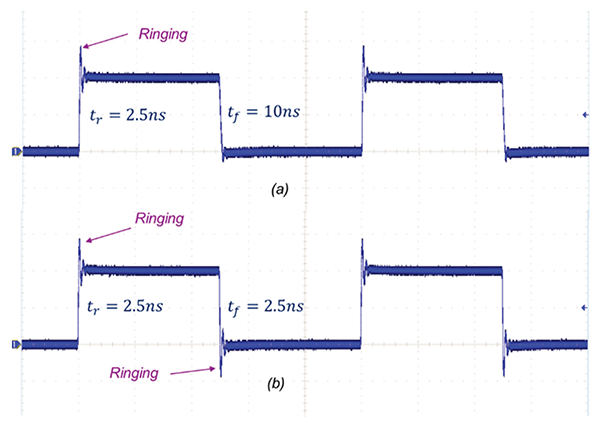
With the rise and/or fall time changed to 2.5 ns we observe a significant ringing present in the system.
Figure 7 shows the expanded view of the ringing waveform on the rising edge.
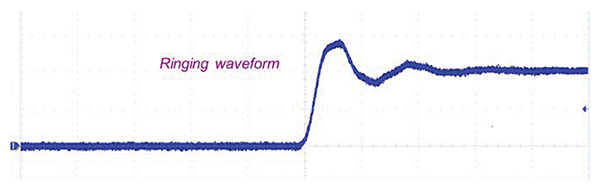
It is evident that the ringing waveform resembles an underdamped sinusoid described by Eq. (4).
It is very instructive and revealing to look at the current waveforms that can be captured using an H-field probe, as shown in Figure 8.

These waveforms are shown in Figure 9 for the 10 ns rise time case, and in Figure 10 for the 2.5 ns rise time case.
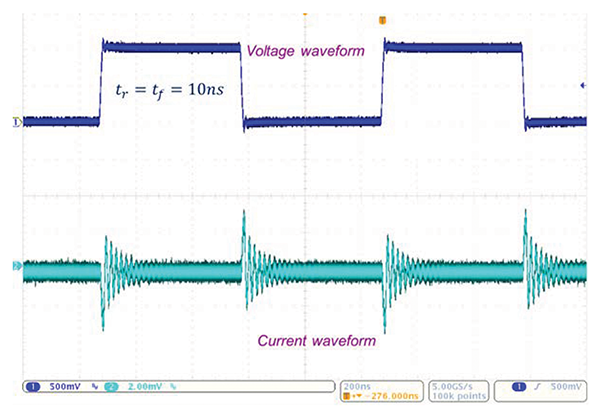
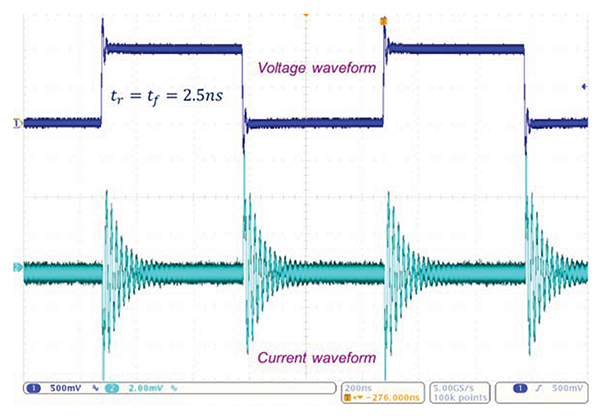
Note that the current waveform exhibits ringing in both cases, while the voltage waveform in the 10 ns case exhibits minimal or no noticeable ringing.
References
- Adamczyk, B., Transmission Line Reflections – Bounce Diagram, In Compliance Magazine, October 2018.
- Adamczyk, B. Foundations of Electromagnetic Compatibility with Practical Applications, Wiley, 2017.
