Editor’s Note: The paper on which this article is based was originally presented at the 2023 IEEE International Symposium on Product Compliance Engineering (ISPCE), held in Dallas, TX in May 2023. It is reprinted here with the gracious permission of the IEEE. Copyright 2024, IEEE.
Introduction
Electrical shock protection is one of the key elements evaluated to ensure product compliance for public safety. As studied and reported by Dalziel [1], the human body physiological effects due to electric shock are determined by how much electrical current passes through the body. Leakage current test requirements provided in UL 101 [2] evaluate the potential body current for utilization equipment and maximizes electrical shock safety. IEC 60990 [3] specifies similar requirements using the same concept but uses a different term, “touch current”. One of the major differences between UL 101 and IEC 60990 is that UL 101 defines the limit and testing procedure measuring the Root-Mean-Square (RMS) value of the leakage current; IEC 60990, on the other hand, defines the limit and testing procedure on the measured peak value of the touch current. The peak limit in IEC 60990 is defined as the RMS limit multiplied by 1.414, which is the standard crest factor for a pure sinusoidal single-frequency waveform. Such criteria agree with each other when the product employs only linear electronic circuits and the measured leakage or touch current is a pure sinusoidal waveform. In the past sinusoidal waveforms were the most common signals encountered but not anymore. Modern technology regularly utilizes nonlinear electronic circuits for many applications such as household appliances, LED lighting, etc., to help improve electrical performance and operating efficiency. Waveforms of the leakage or touch current are, therefore, rarely found to be purely sinusoidal but are typically more complex. Waveforms encountered in modern electric products are more commonly composed of mixed frequency signals and high-peak pulses superimposed on a 60 Hz baseline signal. In these cases, the crest factor between the peak and RMS values is no longer 1.414 but higher and with its value changing based on the waveshape of the leakage current waveform. Therefore, the peak limit and RMS limit are no longer interchangeable in products that use nonlinear electronic circuits. Depending on the specific waveshape, a product could meet the RMS limit but fail to the peak limit. For example, the authors have observed the waveform from a LED tube light was measured at 0.94 MIU in RMS but 7.86 MIU was measured in peak. As the limit in this case (UL 1993 was specified to be 5 MIU RMS (equivalent to 7.07 MIU peak), RMS and peak would give different certification testing results. MIU is a mathematical unit for leakage current measurement using the frequency- sensitive network about which more details can be found in [2] and [4].
The question has been asked for many years: which parameter does the human body respond to: peak or RMS? More experimental research needs to be done to study the comparative effect of peak and RMS values on the human body. In the 1940s, Charles Dalziel conducted human body experiments to study the physiological effects of “the inability to let-go” [1] (or “let-go”) and “perception” [5], and he concluded that the electrical shock physiological effects are controlled by the peak value, not the RMS for 60 Hz sinusoidal waveforms. Dalziel conducted extensive experimental research on the effects of current on the human body and is still cited as an authoritative source for electric shock data; that said, his research has some limitations in scope. For example, most of his experiments were conducted using single-frequency sinusoidal signals when determining the “let-go” current limit for human volunteers [1]. Dalziel did study the effects of other types of waveforms, but these were limited to triangle, square, half-rectified and full-rectified waveforms with a fundamental frequency of 60 Hz. Dalziel also conducted experiments combining a 60 Hz sinusoidal waveform with its third harmonic (180 Hz) set equal to 37.5% of the fundamental when he found peak current as the critical factor in stimulating the human body [6]. In the discussion section of Dalziel’s paper [6], J.A. Dickinson and F.B. Silsbee from the National Bureau of Standards (now the National Institute of Standards and Technology, NIST) questioned the validity of concluding that human body stimulation was controlled by peak current based on a single frequency or combined signals with third harmonics only. Therefore, these foundational tests by Dalziel are not easily relatable to waveforms commonly encountered today and still leave an open question on whether peak or RMS is the more appropriate parameter to assess shock hazards for non-sinusoidal waveforms.
In 1985 Hart reported experimental results comparing the electrical shock sensation of the peak and RMS for mixed- frequency signals [7]. The mixed signals explored by Hart were composed of a 60 Hz fundamental and secondary signal with frequencies between 30 to 100 kHz. Hart conducted testing on “several” people and six different secondary frequency signals and came to a similar conclusion as Dalziel that the peak is the determining factor for physiological effects rather than RMS.
Based on Dalziel and Hart’s experimental results, Perkins demonstrated the complicated leakage/touch current waveforms for various products, including switch mode power supplies, variable speed drives (VSDs), network servers, etc.[8] In his paper, Perkins also demonstrated a method of measuring the peak leakage/touch current value using an oscilloscope and the traditional leakage current measurement network provided in both UL 101 and IEC 60990. In 1997, subsequent work led by Hart and Perkins reported experimental results with human volunteers comparing average, peak, and RMS values of various waveforms with an equivalent 60 Hz sinusoidal (equivalent with respect to perception). The result of this work was included within the American National Standards Institute (ANSI) Standard C101 (now UL 101). In that study, different types of waveforms were considered but only for a single frequency of 60 Hz, which is not a true representation of the practical waveform exhibited by the products nowadays.
Experimental Setup
For this UL Solutions study, a signal mixer/amplifier was used for the experimental work described herein, which had the capability of mixing two higher frequency signals with or without a 60 Hz signal. Using this setup, the reaction frequency factor was measured for each of the two male volunteers and compared with the reaction network factor given in UL 101 and IEC 60990. The customized frequency factor for the particular individual was then used to calculate the equivalent 60 Hz RMS and peak current signals for the mixed frequency signals. The results of this work were then compared with the results obtained using the method by Hart in [7].
Figure 1 shows the experimental setup for the complex waveform study. The power amplifier can mix three individual frequency signals plus a 60 Hz sinusoidal (integrated within the amplifier). The power amplifier has a bandwidth of 100 kHz (−3 dB @ 100 kHz), and the output current is hardware limited to 35 mA for all frequencies for safety considerations. The maximum output voltage was also limited to 120 Vrms for safety. The current pathway was set from the lower arm to the hand (as shown) to mitigate the potential of current passing through the heart. The electrode on the arm consisted of an electronic pad manufactured by TENS for electrotherapy, as shown in Figure 1. The other electrode consisted of a copper cylinder, similar to that used by Dalziel [1] and for work previously published by the authors [9].

Reaction Frequency Factor
In [4], Dalziel conducted human body experiments and measured the threshold of perception for 143 men and 4 women for sinusoidal frequencies from 10 Hz to 200 kHz. The current pathway was from the upper arm (near shoulder) to the hand, which was like that used in this paper (Figure 1). Three different contacts were examined in his investigation: hand hold, finger contact, and finger tap; thresholds of perception were reported for each contact, and statistical results for perception at 5%, 50%, and 95% population were provided.
The leakage current measurement circuit in both UL 101 [2] and IEC 60990 requires the reaction threshold network. It is noted that reaction is a different physiological effect than perception. Perception is an initial sensation of starting to feel the flow of electricity through the body. Reaction is what occurs when the electrical current is high enough for a person to “react” from the energized source. Perception will not likely lead to harmful injury, but reaction can lead to a secondary injury, e.g., falling from a ladder. Like perception, the reaction network is a low-pass filter compensating for the decrease of shock sensation for a given current magnitude as the frequency increases and is based on experimental measurements of perception/reaction as a function of frequency (for example, from Dalziel’s work). It is noted that Dalziel measured the perception threshold, which is a less intense physiological effect than the reaction; therefore, the absolute body current of Dalziel’s results is expected to be lower than the reaction current. This study focused on the reaction effects instead of perception because the reaction current can lead to harmful injuries and the reaction limit is the requirement of both the UL 101 and IEC 60990 standards.
Reaction is here defined as an uncomfortable sensation during which the volunteer reacts to the test current while holding the energized electrode. Several preliminary tests were conducted to familiarize the two test subjects with the sensation of the current at different frequencies. The experiment started with 60 Hz at 1 mA, which is above the perception threshold but lower than the reaction limit which is up to 2 mA. For the first few seconds, the touch current continued to increase due to transient/reactive effects at and near the skin interface. Once the current stabilized at 1 mA, the current was then increased to the reaction sensation of the subject. The subject was asked to memorize this sensation and attempts were made to adjust the current levels throughout this study to recreate the same sensation for all further experiments.
Alternate approaches were considered, such as use of a motion sensor to establish values where reaction was based on a sudden movement of the hand. The motion sensor was not used since the subject knew when the electrode would be energized, and were prepared for that shock sensation, and may still subjectively choose to either react (give up) early or attempt to endure the sensation for longer. Randomly energized plates were also considered but then rejected, as the number of test iterations would need to be high and would be subject to bias and discomfort for the test subjects as there would be anticipation that plates may be energized. Therefore, having the test subject establish a threshold limit and in control of the stimuli was expected to minimize discomfort and maximize consistency in acquiring data, considering that the reaction intensity can be subjective and perceived differently.
Reaction thresholds were measured for two volunteers in the range of frequencies from 60 Hz to 15 kHz. Current thresholds at higher frequencies were not measured due to the maximum output current limitation of the power amplifier and its safety limits. Similar trends were expected based on Dalziel’s results, though measurement of a “personal” reaction curve for each test subject was expected to improve accuracy since results depend on each individual’s perceived sensation while the Dalziel curve is based on a statistical average from a larger population of test subjects.
Figure 2 shows the comparison of frequency factor curves from different sources. Dalziel’s tapping result starts to deviate from the rest above 8 kHz, but the rest of the data follows a similar trend. The frequency factor is calculated using the following equation:
![]()
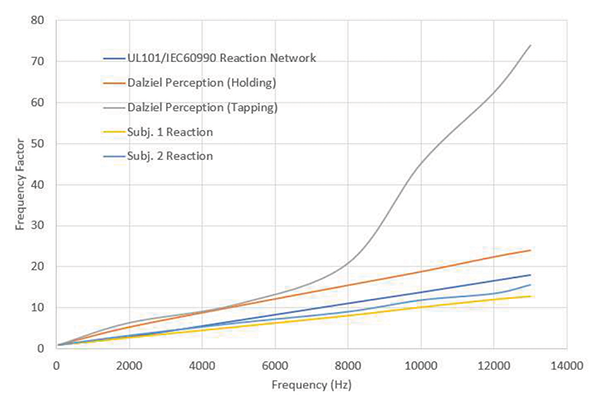
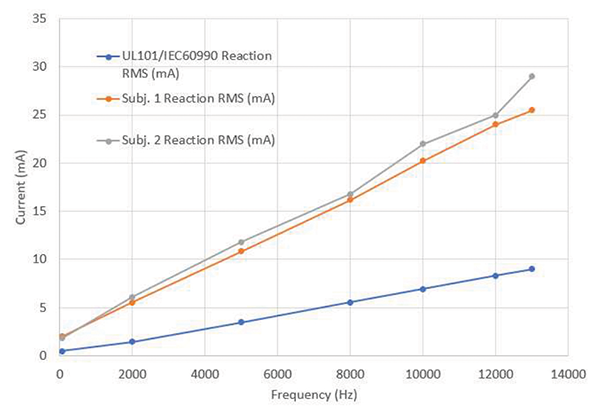
The frequency factor normalizes the reaction for a given frequency relative to the touch current at 60 Hz. Figure 3 shows the measured reaction current for the two test subjects compared with the reaction limit in UL 101, calculated based on the frequency factor. In UL 101, the general reaction current limit is 0.5 MIU. It is noted that MIU is a mathematical unit for leakage current measurement using the frequency sensitive network [2].
As shown in Figure 3, the personal reaction currents were quite close for the two test subjects but higher than the UL 101 threshold limits. This can be understandable since the standard limit is intended to protect 95% of the population from reaction and therefore would typically be more conservative than curves from individuals. The two subjects are both male, between 40 to 50 years old.
Peak vs. RMS
The study described here starts with the same approach taken by Hart in [7]. As referred to in Figure 1, the following steps were taken as the experimental data was collected:
- Adjust the 60 Hz voltage supply to 1 mA through the subject’s arm without a higher frequency component.
- Add the higher frequency component until the current I2 reached 1.414 mA or a fixed current (in [7], Hart used 1.414 mA). Current is reduced relative to Hart in this study since the test subjects found the 1.414 level difficult to tolerate.
- Record I1 and I2 RMS and peak value.
- Reduce the high-frequency component to zero.
- Increase the 60 Hz current until the test subject reported the same feeling of intensity as the mixed-signal current; record I1 and I2 RMS and peak value.
Results and Discussion
In these measurements, I1 is the actual body current going through the arm in mA; I2 is the theoretical current passing the resistor R1 in MIU, which can be expressed by:
![]()
The parallel RC circuit implements Dalziel’s frequency factor as a low-pass filter. For 60 Hz signals, I2 equals I1. At a higher frequency above 60 Hz, I2_Mixed shall be equal to the current I2 with only the 60 Hz signal if the reaction network can translate the shock sensation perfectly. Nevertheless, a deviation exists between the current I2 of the mixed signal and the equivalent 60 Hz current with the same shock sensation for either RMS or peak. The deviation percentage is introduced to differentiate the effectiveness of the measurement to evaluate the shock sensation using a 60 Hz current limit. This deviation percentage quantifies the difference between the 60 Hz signal set by the test subject at the same perceived intensity level as the mixed signal and the actual level of the mixed signal to determine which parameter better predicts the shock intensity. The deviation percentage for either RMS or peak is calculated as:
![]()
Therefore, the deviation percentage quantifies the difference between the perception of the test subject with the predicted perception level based on the frequency factor filter network. A smaller deviation implies that the frequency factor more accurately predicts 60 Hz equivalency for mixed frequencies.
Table 1 shows a sample result of an experiment for Subject 1. Current I1 is the actual touch current of the high-frequency component required for current I2 to reach 1.414 mA. Current I2 is the total current after the Dalziel frequency network (low pass filter; therefore, this value gives a signal magnitude normalized to 60 Hz equivalent). The current I2 is not the true current passing through a human body but is normalized by the reaction filter network to scale to 60 Hz equivalent. Therefore, if the Dalziel reaction network predicted the shock sensation perfectly, current I2 shall equal to the 60 Hz only current (column 5) with the same shock sensation, and the deviation percentage would be zero. The RMS and peak of the equivalent 60 Hz-only current are shown with the same shock sensation of the mixed signal. Table 1 shows measured values and calculated deviation percentages for a single set of experiments for Subject 1.
| HF | 60 Hz | HF/1 RMS (mA) | Mixed/2 RMS (mA) | /2 Peak (mA) | 60 Hz Measured Perception, RMS (mA) |
60 Hz Measured Perception, Peak (mA) |
Deviation Percentage, RMS | Deviation Percentage, Peak |
| 2 kHz | 1 mA | 2.7 | 1.41 | 3 | 1.70 | 2.75 | 17.06% | 9.09% |
| 5 kHz | 1 mA | 6.7 | 1.41 | 3 | 1.82 | 2.935 | 22.53% | 2.21% |
| 8 kHz | 1 mA | 11 | 1.41 | 3 | 1.90 | 3.06 | 25.79% | 1.96% |
| 10 kHz | 1 mA | 13.7 | 1.41 | 3 | 2.00 | 3.2 | 29.50% | 6.25% |
| 12 kHz | 1 mA | 16.7 | 1.41 | 3 | 2.00 | 3.2 | 29.50% | 6.25% |
Table 1: Results examples for Subject 1 via Dalziel Reaction Network
Table 2 presents the comparison of RMS and peak results, using Dalziel and personal reaction curves for the two subjects. Overall, the peak showed a lower deviation than RMS values. For Subject 2, using the personal reaction curves significantly improves results, as the Dalziel curve gives inconsistent results across the frequency range. For Subject 1, personal and Dalziel reaction curves do not exhibit a significant change in the results. The use of personal reaction curves improves the RMS results for both test subjects, but the values are higher than the corresponding peak values. Though these initial results support the hypothesis that peak better characterizes perception/ reaction levels across multiple frequencies, additional data is needed on a larger sample set of test subjects, as well as using additional complex waveforms (including those with more than two sinusoidal components as well as waveforms found in modern appliances) before making a conclusion whether peak or RMS values better characterize perception and reaction levels across multiple frequencies.
| Subject 1 | Subject 2 | |||||||
| HF | Personal Reaction Curve | Dalziel Reaction Curve | Personal Reaction Curve | Dalziel Reaction Curve | ||||
| RMS | Peak | RMS | Peak | RMS | Peak | RMS | Peak | |
| 2 kHz | 17.65% | 1.82% | 17.06% | 9.09% | 18.06% | 2.69% | 9.03% | 16.73% |
| 5 kHz | 9.34% | 11.28% | 22.53% | 2.21% | 15.66% | 2.75% | 15.06% | 10.09% |
| 8 kHz | 12.11% | 7.84% | 25.79% | 1.96% | 14.37% | 4.21% | 18.97% | 5.26% |
| 10 kHz | 15.00% | 4.69% | 29.50% | 6.25% | 12.43% | 5.36% | 16.57% | 7.14% |
| 12 kHz | 13.00% | 6.56% | 29.50% | 6.25% | 15.17% | 2.03% | 20.79% | 1.69% |
| Mean | 13.42% | 6.44% | 24.88% | 5.15% | 15.14% | 3.41% | 16.08% | 8.18% |
| Median | 13.00% | 6.56% | 25.79% | 6.25% | 15.17% | 2.75% | 16.57% | 7.14% |
| Std Dev | 0.0312 | 0.0353 | 0.0525 | 0.0303 | 0.0205 | 0.0135 | 0.0451 | 0.0567 |
Table 2: Comparison of personal and Dalziel filter
References
- C. Dalziel, E. Ogden, and C. Abbott, “Effect of Frequency On Let-go Currents,” AIEE Transactions in Electrical Engineering, vol. 62, pp. 745-750, December 1943.
- UL 101, “UL Standard for Safety for Leakage Current For Utilization Equipment,” 6th Ed., 2019.
- IEC 60990, “Methods of Measurement of Touch Current and Protective Conductor Current,” 3rd Ed., May 2016.
- Hai Jiang, “Study of High-Frequency Spectrum for 120 V Household Appliances,” UL White Paper, April 2023.
- C. Dalziel, and T. H. Mansfield, “Effect of Frequency On Perception Currents,” AIEE Transactions in Electrical Engineering, vol. 69, Issue 2, pp. 1162-1168, January 1950.
- C. Dalziel, J. Lagen, and J. Thurston, “Electric Shock,” AIEE Transactions in Electrical Engineering, vol. 60, pp. 1073-1079, December 1941.
- W.F. Hart, “A Five-Part Resistor-Capacitor Network for Measurement of Voltage and Current Levels Related To Electric Shock and Burns,” Electrical Shock Safety Criteria, Proceedings of the First International Symposium on Electrical Shock Safety Criteria, pp. 183-192, 1985.
- P. Perkins, “What does your touch current look like? Making proper touch current measurements,” IEEE Symposium on Product Compliance Engineering (ISPCE) Measurements, May 2014.
- H. Jiang and P. Brazis, “Experiments of DC human body resistance I: Equipment, setup, and contact materials,” IEEE Symposium on Product Compliance Engineering (ISPCE), May 2018.
