This month the concept of near and far fields will be explained using simple theory and examples. Of course, a detailed and precise explanation is not the scope of this article so, please, consider reviewing a book in electromagnetics with Maxwell theory for a complete and precise overview.
In EMI/EMC we work with antennas measuring in the far field, we compare electric field levels in far field with legal limits, we troubleshoot circuits with near field probes, etc.
What is the meaning of near and far? As usual in EMI/EMC fields, it depends.
First important idea is to remember that any electromagnetic wave has impedance, the wave impedance. Wave impedance Zw is the ratio between electric (V/m) and magnetic (A/m) fields for that wave. So Zw = E/H. Note that V/m divided by A/m are ohms.
So, if the signal you are measuring has 10V/m in electric field and 0.04A/m in magnetic field, your wave has 250ohms Zw wave impedance.
In this way, signals with high E value and low H value are high impedance waves and signals with low E value and high H value are low impedance waves (note the equivalent point of view when using circuit theory approach: circuits with high voltage and low current are high impedance circuits and those with low voltage and high current are low impedance circuits).
Second idea is to remember that electric and magnetic fields are attenuated as you increase the distance to the source. So, for the circuit in Figure 1, electric (E) and magnetic fields (H) decrease in amplitude as you go far from the circuit.
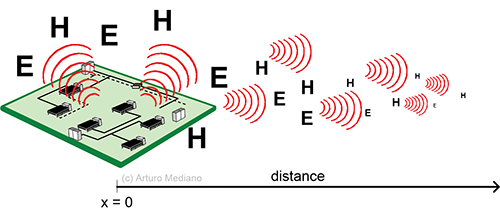
Close to the origin of the signal, E and H are bigger. As you go far from the circuit E and H are attenuated as 1/x, 1/x2, or 1/x3 where x is distance to source.
Note that only signals radiated will be able to arrive far from the circuit (when your circuit has some desired or undesired antenna for them). Other signals will be around the components in your circuit without the possibility to be radiated (this is stored energy).
How is the ratio between E and H (the wave impedance) as you are far or close to the origin of the signal?
Consider your circuit is located in position X=0 in Figure 2. The graph is plotting the wave impedance Zw=E/H. When you are very far (i.e. d>λ) from your circuit the ratio you will be measuring between E and H will be exactly Zo=377Ω. This is the wave impedance in the ar field. So, when in the far field, if you know the electric field level, you can easily calculate the magnetic field amplitude. Increasing distance, the ratio is constant because in the far field both E and H are attenuated with 1/x.
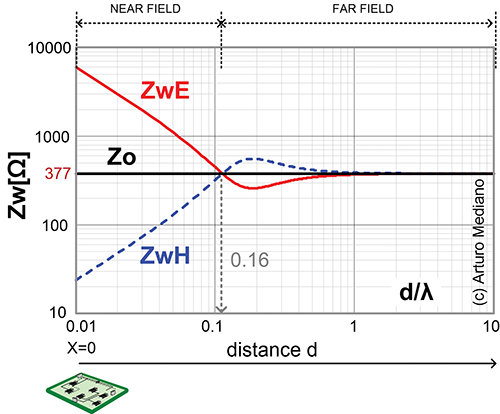
In that situation, you will not be able to know if the origin of the signal is a low impedance circuit (i.e. loop) or a high impedance circuit (i.e. an open wire). You are receiving in the far field a plane wave and we use antennas to receive those signals.
Now, consider you go closer to the circuit. You will see that E/H is around 377 ohms but when distance goes to approximately λ/6 (d/ λ=0.16) the ration E/H will start to increase or decrease from the Zo value.
What you will see is that wave impedance will take values close to the impedance of the circuit we created the signals. For example, if the signal was created by a low impedance circuit as a loop (high current – low voltage), Zw will decrease from 377 ohms as you get closer to the circuit. If the signal was created by a high impedance circuit as an open wire (high voltage – low current), Zw will increase from 377 ohms as you get closer to the circuit.
That is because in the near field we do not use antennas, we use near field magnetic or electric probes.
For example, think you have a circuit creating a radiated problem at 250MHz. For that frequency, λ/6 is 20cm. So, if you measure/receive the signal at 5 meters, you will be in the far field. If you measure/receive the signal at 5cm, you will be in the near field (Figure 3).
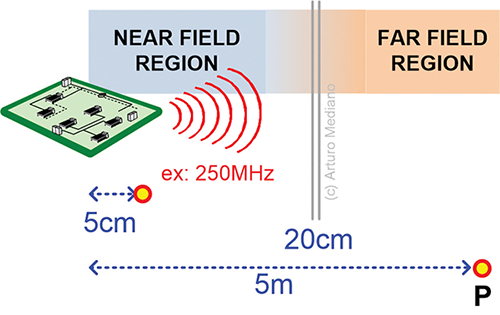
It is important to understand that the far field value is related with the near field values, but, if you measure signals in the near field, perhaps you will not detect those signals in the far field simply because they could not be radiated (they are stored in the area where you are measuring but there is not some kind of antenna sending the signal to far distances).
The topic of near and far fields is very important in EMI/EMC because is critical to know what kind of probe you need for measuring, how effective will your shielding be at some specific frequency, how is the origin of a signal being radiated, etc.
My final recommendation: try to calculate the near to far field distance in your application for a better understanding of your problems.

