Highest Significant Frequency, Electrically Short Structures, and Transmission Line Criterion

This article discusses the origins, justification, and interrelations between some of the basic EMC rules regarding the highest significant frequency (bandwidth) present in digital signals, the definition of the electrically short structures, and the transmission line criterion. The analytical basis and the interrelations between these rules are discussed, followed by the simulation and measurement results.

Highest Significant Frequency (Signal Bandwidth)

Consider a trapezoidal clock signal shown in Figure 1.

When the rise and fall times are equal, the one-sided Fourier spectrum of the trapezoidal clock signal can be represented as

  (1)

where the magnitudes of the (complex) Fourier coefficients are given by [1]

  (2)

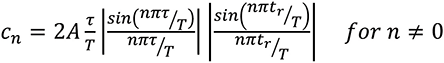  (3)

The angle of the Fourier coefficients is given by

  (4)

The spectral coefficients in Eq. (3) exist only at the discrete frequencies f = n/T. The continuous envelope of these spectral components is obtained by replacing n/T = f  in Eq. (3):

  (5)

or in dB,

  (6)

The (envelope) bounds in dB are shown in Figure 2.

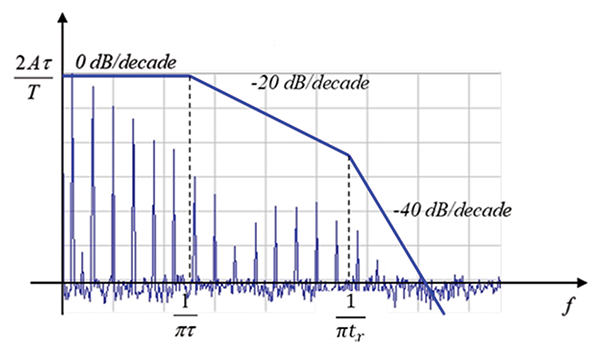
Note that above the frequency f = 1/π t_r the amplitudes of the spectral components are attenuated at a rate of 40 dB/decade. It seems, therefore, reasonable, to postulate that somewhere above this frequency these amplitudes are negligible (as compared to the magnitudes of the components at lower frequencies) and can be neglected in the Fourier series expansion shown in Eq. (1).

A reasonable choice for that frequency is [1]

  (7)

This is the origin of one of the EMC rules which state that the bandwidth (BW) of a trapezoidal signal (the highest significant frequency) is

  (8)

With this choice of the highest significant frequency given by Eq. (8) infinite summation in Eq. (1) can be replaced by the upper limit of N, where N corresponds to the highest harmonic up to the maximum frequency in Eq. (8), i.e.,

  (9)

Let’s check the validity of this criterion for a 1V, 50% duty cycle, 10 MHz trapezoidal signal with a rise time of 2.5 ns (i.e., the bandwidth of 400 MHz).

Figure 3 shows the results of the summation in Eq. (9) with N = 20, (harmonics up to the half of the highest significant frequency).

Note the overshoot and ringing present in the reconstructed signal. Next, let’s sum up all the harmonics up the value of the f_max, i.e. for N = 40. This is shown in Figure 4.

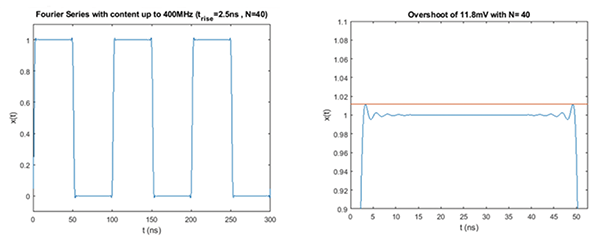
We note a visible improvement in the signal integrity. To complete the verification, let’s sum up all the harmonics up the value of the 2 f_max, i.e. for N = 80. This is shown in Figure 5.

While we see further improvement in the reconstructed signal, the improvement is not as significant as from N = 20 to N= 40. We conclude that the simulation results agree with the criterion in Eq. (8).

Let’s verify this by the spectral measurements (see [2] for the measurement setup). Figure 6 shows the frequency spectrum of a 10 MHz, 1V, trapezoidal clock signal with a rise and fall times equal to 2.5 ns.

Superimposed on the spectrum are two straight lines connecting the peaks of the spectrum. Note that the slopes of these lines conform to the envelope slopes shown in Figure 2. The breakpoint where the peak slope changes from 20 dB to 40 dB is at f = 2/π⊇t_r validating the theoretical conclusion that past the frequency f = 1/t_r the amplitudes of the frequency spectrum are attenuated at 40 dB/decade.

Insignificant Transmission Line Effects

Transmission lines introduce time delays and produce reflections (when the line is not matched). A very important question to ask is: when are these effects insignificant, i.e. when the line does not need to be treated as a transmission line?

To answer this question, consider a circuit shown in Figure 7, with the time delay (one-way travel time) is T_D = 9 ns.

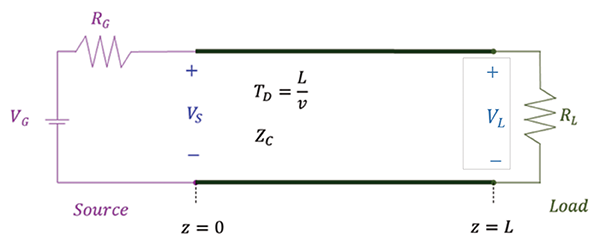
Let the source signal be a pulse with variable rise time. Figure 8 shows the voltages at the source and the load with the rise time t_r = 2.5 ns, (see [3] for the measurement setup).

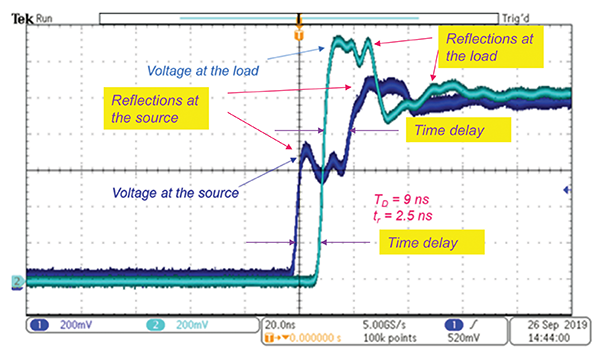
We observe a noticeable time delay and reflections at the source and the load [4]. Figure 9 shows the voltages at the source and the load with the rise time t_r = 10 ns.

Note that the time delay and the reflections become smaller. Let’s increase the rise time to 50 ns. The result is shown in Figure 10.

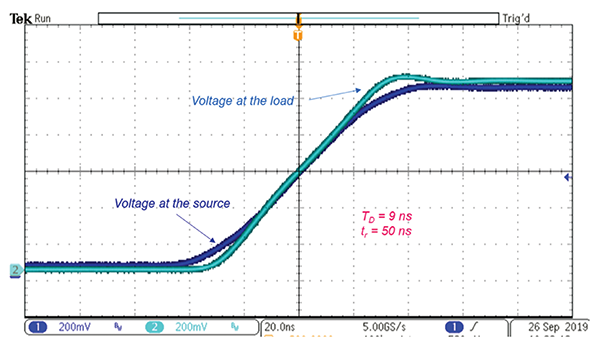
Notice the further decrease in the time delay and reflections. Finally, let’s increase the rise time to 100 ns. The result is shown in Figure 11.

The results shown in Figure 11 indicate that the transmission line effects are negligible. This leads us to the (time-domain) transmission line criterion:

The line does not need to be treated as a transmission line when the pulse rise time t_r is greater than, or equal to, 10 times one-way time delay T_D of the line.

  (10)

Next, we will derive an equivalent frequency domain criterion.

Electrical Length

Recall from Eq. (8) that the highest significant frequency present in a pulse signal is

  (11)

Using Eq. (11) in Eq. (10) we get

  (12)

The one-way time delay T_D is related to the line length, L, and the velocity of propagation, v, by

  (13)

Using Eq. (13) in Eq. (12) we get

  (14)

or

<  (15)

The wavelength λ is related to the velocity of propagation, v, and the frequency f by

  (16)

Using Eq. (16) in Eq. (15) we get

  (17)

We have arrived at the (frequency domain) transmission line criterion:

The line does not need to be treated as a transmission line when its length L is smaller than, or equal to λ/10, where λ is the wavelength at the highest frequency of interest.

The condition in Eq. (17) is also the criterion for the electrically short structures.

A physical structure, or a physical distance, is considered electrically short when its physical length L is smaller than, or equal to λ/10, where λ is the wavelength at the highest frequency of interest.

References

1. Clayton R. Paul, Introduction to Electromagnetic Compatibility, Wiley, 2006.
2. Adamczyk, B., “Spectra of Digital Clock Signals,” In Compliance Magazine, April 2017.
3. Adamczyk, B., “Transmission Line Reflections at a Resistive Load,” In Compliance Magazine, January 2017.
4. Adamczyk, B. Foundations of Electromagnetic Compatibility with Practical Applications, Wiley, 2017.