This Part II of the tutorial illustrates the Bode plots’ use in several EMC applications (see Part I, [1], for the fundamentals of Bode plots). EMC applications will include the non-ideal models of resistors, inductors, and capacitors, as well as the spectral bounds on digital clock signals.
Non-Ideal Models of Passive Circuit Components
Resistor
Circuit model of a resistor and its parasitics is shown in Figure 1 [2].
Let’s obtain the straight-line Bode plots approximations of the magnitude of the impedance of this resistor vs. frequency, with respect to nodes A and B. For this case, the details of derivations will be shown, leading to the final plots. In the subsequent discussion of an inductor and a capacitor, the details will be omitted as the derivations follow a similar pattern.
The impedance transfer function for the circuit shown in Figure 1 is
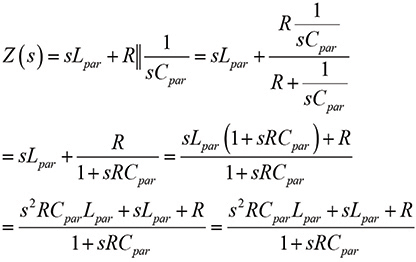 (1a)
(1a)
or
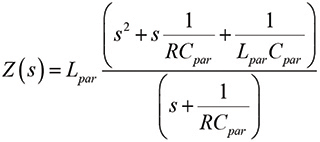 (1b)
(1b)
The magnitude of the frequency transfer function is obtained as
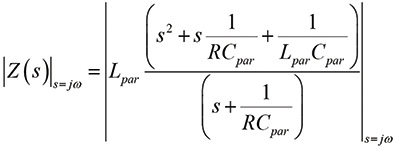 (2a)
(2a)
or
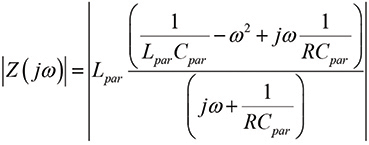 (2b)
(2b)
Eq. (2b) can be written as
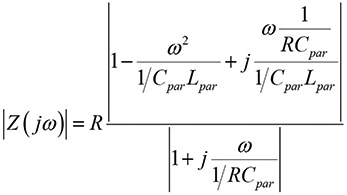 (2c)
(2c)
or in dB as
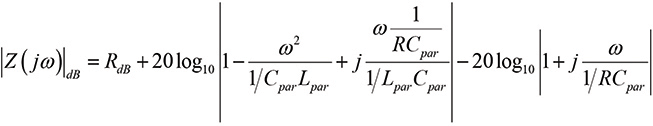 (3)
(3)
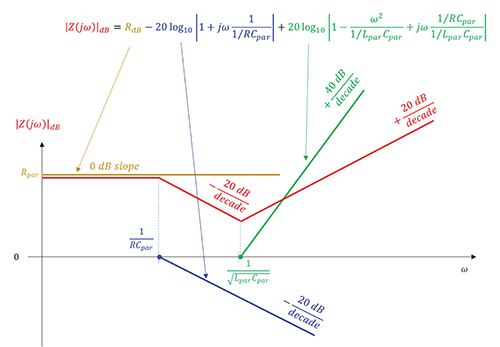
Recall from [1]: Bode plot of a constant R is a straight horizontal line at a value of RdB.
The straight-line approximation to the second term in (3) consists of two asymptotes: 0 dB line until the frequency ![]() and a +40 dB/decade line beyond that frequency.
and a +40 dB/decade line beyond that frequency.
The straight line approximation to the third term in (3) consists of two asymptotes: 0 dB line until the frequency ![]() and a -20 dB/decade line beyond that frequency.
and a -20 dB/decade line beyond that frequency.
Note: the values of the corner frequencies for the second and third term can be directly obtained by inspection from the impedance transfer function in (1b).
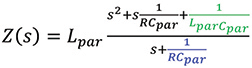 (4)
(4)
Caution: In order to identify these values by inspection the coefficients of the highest powers of the polynomials in s both in the numerator and in the denominator must be equal to 1.
The value of the constant R can be obtained from (1b) as [1]
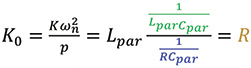 (5)
(5)
We are now ready to construct the Bode plot of the magnitude of the impedance of a non-ideal resistor, as shown in Figure 2.
Inductor
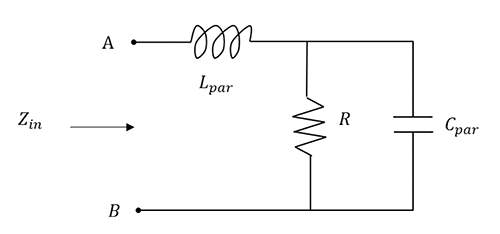
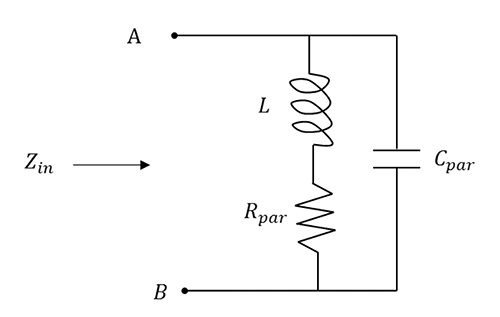
Circuit model of an inductor and its parasitics is shown in Figure 3 [2].
The impedance transfer function for the circuit shown in Figure 3 is
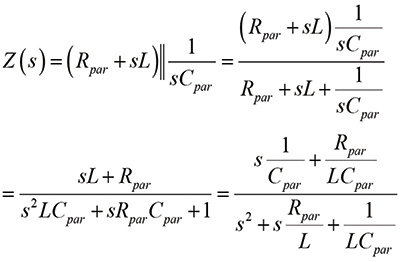 (6a)
(6a)
or
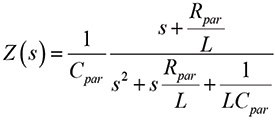 (6b)
(6b)
The values of the corner frequencies for the first order term in the numerator and the second order term in the denominator are obtained directly from (6b) by inspection as
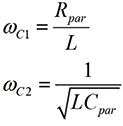 (7a)
(7a)
The value of the gain constant is [1]
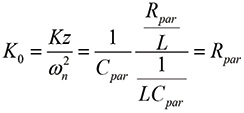 (7b)
(7b)
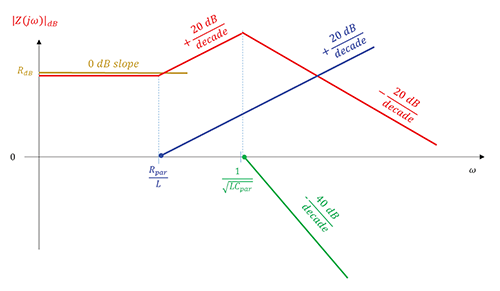
Bode plot of the constant Rpar is a straight horizontal line at that value in dB.
The straight line approximation to the first order term in the numerator of (6b) consists of two asymptotes: 0 dB line until the frequency ![]() and a +20 dB/decade line beyond that frequency.
and a +20 dB/decade line beyond that frequency.
The straight-line approximation to the second order term in the denominator of (6b) consists of two asymptotes: 0 dB line until the frequency ![]() and a -40 dB/decade line beyond that frequency.
and a -40 dB/decade line beyond that frequency.
We are now ready to construct the Bode plot of the magnitude of the impedance of a non-ideal inductor, as shown in Figure 4.
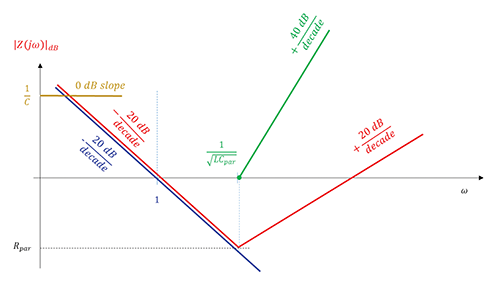
Circuit model of a capacitor and its parasitics is shown in Figure 5 [2].
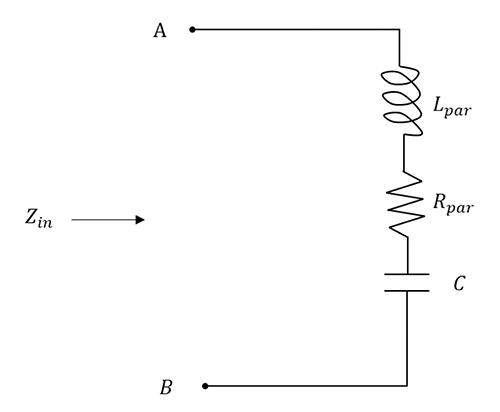
The impedance transfer function for the circuit shown in Figure 5 is
 (8a)
(8a)
or
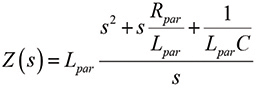 (8b)
(8b)
The value of the corner frequency for the second order term in the numerator is obtained directly from (8b) by inspection as
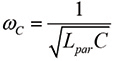 (9a)
(9a)
The denominator represents a straight line on a Bode plot crossing the frequency axis at ω = 1.
The value of the gain constant is
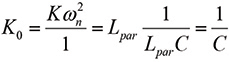 (9b)
(9b)
Bode plot of the constant 1/C is a straight horizontal line at that value in dB.
The straight-line approximation to the second order term in the numerator of (8b) consists of two asymptotes: 0 dB line until the frequency ![]() and a +40 dB/decade line beyond that frequency.
and a +40 dB/decade line beyond that frequency.
The straight line (exact) plot to the first order pole in the denominator of (8b) consists of a straight line of a slope -20 dB/decade crossing the frequency axis ω = 1.
We are now ready to construct the Bode plot of the magnitude of the impedance of a non-ideal capacitor, as shown in Figure 6.
Spectral Bounds of Digital Clock Signals
Digital clock waveforms can be represented as periodic trains of trapezoid-shaped pulses as shown in Figure 7.
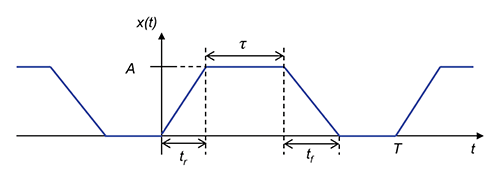
Each pulse is described by the key parameters: period T (and thus the fundamental frequency f0 = 1/T), amplitude A, rise time tr, fall time tf, and the on-time or pulse width τ. When the rise and fall times are equal, the one-sided Fourier spectrum of the trapezoidal clock signal can be represented as
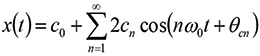 (10)
(10)
where the magnitudes of the (complex) Fourier coefficients are given by [3]
![]() (11)
(11)
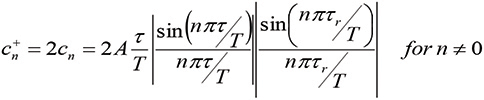 (12)
(12)
The spectral coefficients in Eq. (12) exist only at the discrete frequencies f = n/T. The continuous envelope of these spectral components is obtained by replacing n/T = f in Eq. (12):
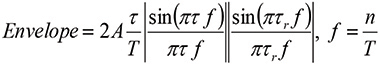 (13)
(13)
or in dB,
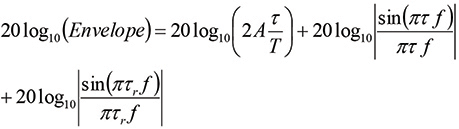 (14)
(14)
Since
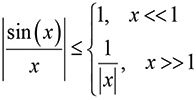 (15)
(15)
It follows that
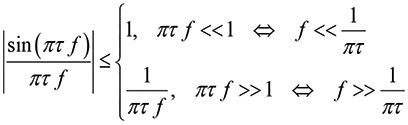 (16a)
(16a)
and
 (16b)
(16b)
The straight line approximation of the term in Eq. (16a) is a 0 dB line until the frequency f = 1/π τ and a -20 dB/decade line beyond that frequency.
The straight line approximation of the term in Eq. (16b) is a 0 dB line until the frequency f = 1/π τr and a -20 dB/decade line beyond that frequency.
The (envelope) bounds in dB corresponding to Eq. (14) are shown in Figure 8.

References
- Bogdan Adamczyk, “Basic Bode Plots in EMC Applications – Part I – Fundamental Background,” In Compliance Magazine, April 2019.
- Adamczyk, B., Teune, J., “Impedance of the Four Passive Circuit Components: R, L, C, and a PCB Trace,” In Compliance Magazine, January 2019.
- Bogdan Adamczyk, “Spectra of Digital Clock Signals,” In Compliance Magazine, April 2017.
