This is the last of the three articles devoted to the topic of a Smith Chart. The previous two articles, [1,2], introduced the concept of normalized load impedance leading to the resistance and reactance circles, which in turn were used to locate the normalized load impedance on the Smith Chart. This article explains how to use a Smith Chart to determine the input impedance to transmission line at a given distance from the source or the load.
Recall the two typical circuit models of a transmission line [1]. In Model 1, shown in Figure 1. The source is located at z = 0, and the load is located at z = L.
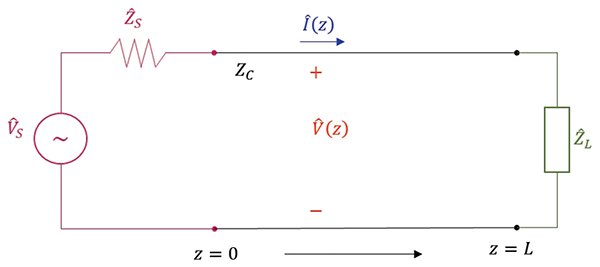
In Model 2, shown in Figure 2, the load is located at d = 0, and the source is located at d = L.
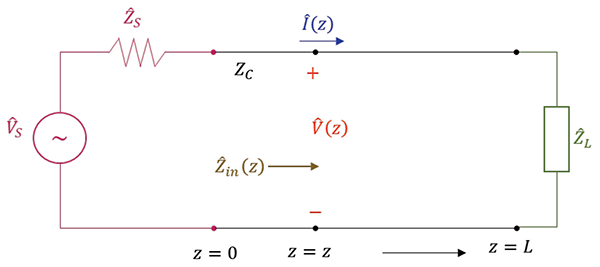
In either model, the input impedance to the line at any location is always calculated looking towards the load. Recall from [3]: The input impedance to the line at any location d away from the load can be obtained from
(1)
where 
(d) is the voltage reflection coefficient at any location d, away from the load, and can be expressed in terms of the load reflection coefficient as
(2)
The load reflection coefficient can be expressed in terms of its magnitude and angle as
(3)
Utilizing Eq. (3) in Eq. (2) we obtain
(4)
We refer to (d) as the phase-shifted load reflection coefficient. Note that the phase-shifted load reflection coefficient has the same magnitude as the load reflection coefficient, but the phase of (d) is shifted by relative to the phase of L.
On the Smith Chart, obtaining (d) from L means keeping the magnitude, ΓL, constant and decreasing the phase by 2βd. Phase decrease corresponds to the clockwise rotation on the Smith Chart. This is shown in Figure 3.
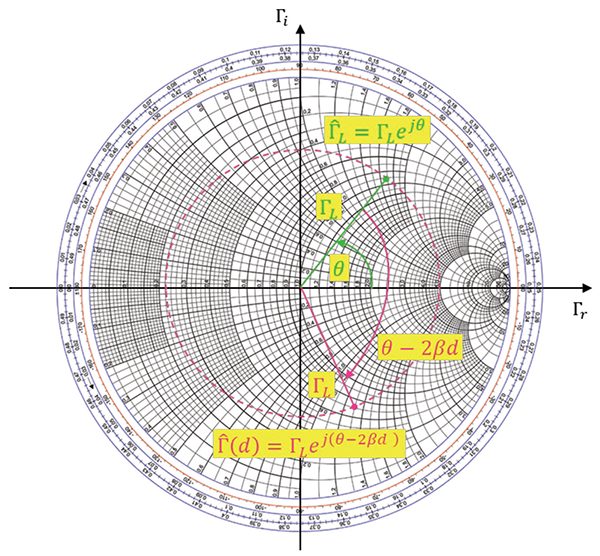
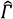L into (d)Let’s return to Eq. (1). Dividing both sides by the characteristic impedance of the line, ZC , we obtain the normalized input impedance to the line at any location d away from the load,
(5)
or
(6)
Let’s compare this expression with the one for normalized load impedance, [2],
(7)
The mathematical form of these two equations is the same! If L is replaced by (d) then 
L gets replaced by in(d).
On the Smith Chart obtaining in(d) from L means keeping the magnitude of L constant and decreasing the phase by 2βd. This is shown in Figure 4.
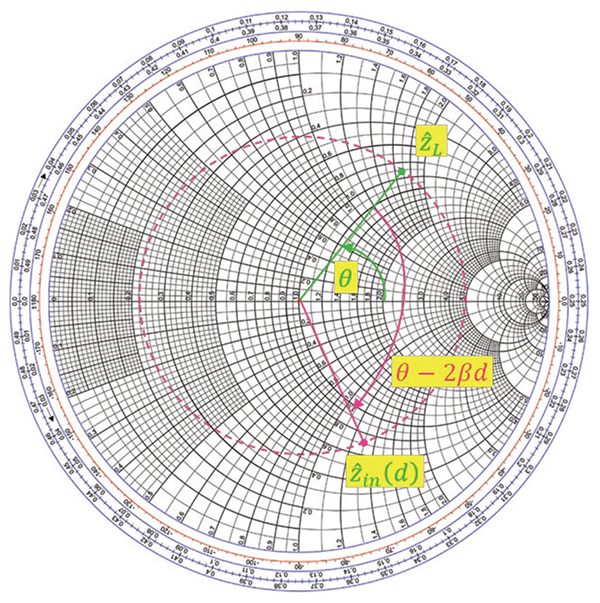
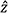L into 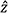in(d)When using Smith Chart, the distance d is expressed in terms of wavelengths. A complete rotation around the Smith Chart corresponds to a phase change of 360° or 2π radians.
(8)
The phase constant β is related to the wavelength λ by
(9)
Thus
(10)
from which
(11)
This means that one complete rotation around the Smith Chart corresponds to the distance change of λ/2. The rotation around the Smith Chart, either in degrees or wavelengths, is denoted on the outer three scales around its perimeter, as shown in Figure 5.
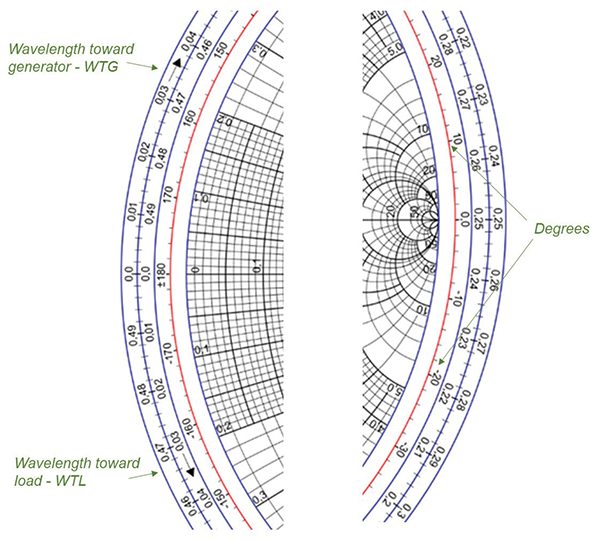
We have shown how to obtain in(d), the normalized input impedance to the line at a distance d away from the load. What about in(z), the normalized input impedance to the line at a distance z away from the source?
in(z) can be easily obtained from in(d) since the two distance variables are related by, [3,4],
(12)
Thus, if we are given z, the distance from the source, we can calculate d, the corresponding distance from the load, and use the procedure just described to obtain the input impedance to the line at that location.
In summary, to determine the input impedance to the line at any distance from the load or the source, using Smith Chart, the following steps need to be taken:
Calculate the load reflection coefficient
(13)
Obtain the normalized load impedance
(14)
Locate this impedance on the Smith Chart at the intersection of the resistance and reactance circles.
Calculate the distance from the load, d, or the source, z, in terms of wavelengths.
To obtain the normalized input impedance to the line at a distance d from the load, move clockwise on the constant radius circle from L.
Multiply the normalized input impedance by the characteristic impedance of the line, ZC, to obtain the actual input impedance.
(15)
References
- Adamczyk, B., “Smith Chart and Input Impedance to Transmission Line – Part 1: Basic Concepts,” In Compliance Magazine, April 2023.
- Adamczyk, B., “Smith Chart and Input Impedance to Transmission Line – Part 2: Resistance and Reactance Circles,” In Compliance Magazine, May 2023.
- Adamczyk, B., “Sinusoidal Steady State Analysis of Transmission Lines – Part II: Voltage, Current, and Input Impedance Calculations – Circuit Model 1,” In Compliance Magazine, February 2023.
- Adamczyk, B., “Sinusoidal Steady State Analysis of Transmission Lines – Part III: Voltage, Current, and Input Impedance Calculations – Circuit Model 2,” In Compliance Magazine, March 2023.
