The two primary shielding mechanisms are reflection and absorption. The two combined result in the familiar expression SE(dB) = R(dB) + A(dB), where SE(dB) is shielding effectiveness in decibels, R represents Reflection Loss, and A represents Absorption Loss (both also expressed in decibels). Often, absorption loss (also called penetration loss) is the energy that is not first reflected by the shield that is absorbed by it – the topic of this article.
Note: A third term involved in the SE equation called the multiple reflection factor B is often ignored if A is greater than 9 dB or if the field is electric or plane wave.
Absorption Loss Dependences for EMI Shields
It does not matter if the field impinging upon a shield is electric, magnetic, or simply a plane wave, the distance from the shield, or its wave impedance; the absorption loss the shield achieves depends entirely on the barrier thickness and skin depth. Barrier thickness is self-explanatory; however, the concept of skin depth is a little more complicated.
The Concept of Skin Depth
If you’re involved with compliance engineering, you should have a pretty good understanding of skin depth. It is a topic of great discussion that often arises around office cubicles and water coolers of most engineering spacings. And if you are a compliance or EMC engineer, you’ll be expected to know it regarding absorption loss and other areas.
Skin depth (or skin effect as it is often called) is the distance required for the impinging wave to be attenuated to 1⁄e or 37% of its original value, where e, Euler’s number (pronounced “Oiler”), equals approximately 2.71828.
The equation for skin depth in meters (m) is:
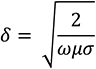
where:
δ = Skin depth
w = 2πf (f is frequency)
μ = permeability of the shielding material
σ = conductivity of the shielding material
Skin Depth and Absorption Loss
If it is not obvious, the above equation indicates that absorption loss is caused by a decrease in shield current through the material due to skin depth and that the losses are affected primarily by two material properties, namely permeability and conductivity.
Also, notice the square root of frequency term in the above equation. This means that as frequency increases, absorption becomes the dominant term exponentially.
A useful formula for determining absorption loss (A) in dB is 8.69 * (t/δ) where t is barrier thickness and δ is skin depth. This means that absorption loss in a shield one skin depth thick is approximately 9 dB, and doubling the thickness of the shield results in double the amount of absorption loss in dB. Note also that there is no “20 log” term because skin depths are exponential and the log of an exponential function is a linear function.
Skin Depths of Various Materials
To determine a shielding material’s potential absorption loss capability, you must first know the frequency or frequencies of concern and, second, what shield materials you have available. The skin depth of copper will be different from that of aluminum, which is different from steel, depending on frequency. For instance, steel offers greater absorption capability than copper at lower frequencies with high relative permeability. But perhaps you do not care about shielding effectiveness at lower frequencies so you can use a more cost-effective material, such as aluminum. This will require some research and I suggest putting it all in a table for easy comparison. Still, steel is generally better than copper at providing absorption loss; however, at low frequencies (~ 1000 Hz), a thick sheet of steel must be used to provide adequate absorption loss.
Summary
Absorption loss in shielding materials is proportional to thickness and inversely proportional to skin depth due to a decrease in shield current through the material. Skin depth is determined further by the permeability and conductivity of the material. Steel is better than copper at providing absorption loss.
References and Further Reading
- Williams, T., EMC for Product Designers, 5th Edition, Newnes, 2017.
- Kimmel Gerke Associates, Ltd., EDN Designer’s Guide to Electromagnetic Compatibility, 2005.
- Ott, H.W., Electromagnetic Compatibility Engineering, Wiley, 2009.
