Editor’s Note: The paper on which this article is based was originally presented at the 2014 IEEE EMC Symposium, where it received recognition as the Best Symposium Paper. It is based on work sponsored by the U.S. Government and is not protected by copyright in the U.S. However, copyright outside of the U.S. is held by the IEEE, which has graciously granted us permission to reprint it here.
 Radio-frequency (RF) wireless communications and sensor networks are currently being deployed in structures that comprise confined, reflective spaces that are electromagnetically coupled together via apertures, seams, and bulkhead cable and pipe penetrations. Such structures are commonly found in aviation, shipping, automotive, and warehousing industries [1], [2]. It is necessary to understand the propagation of RF energy through these coupled reverberant spaces. The highly multipath electromagnetic environment created from RF emissions into the wireless channel can be identified as a cause of electromagnetic interference to electronic equipment systems installed in these spaces.
Radio-frequency (RF) wireless communications and sensor networks are currently being deployed in structures that comprise confined, reflective spaces that are electromagnetically coupled together via apertures, seams, and bulkhead cable and pipe penetrations. Such structures are commonly found in aviation, shipping, automotive, and warehousing industries [1], [2]. It is necessary to understand the propagation of RF energy through these coupled reverberant spaces. The highly multipath electromagnetic environment created from RF emissions into the wireless channel can be identified as a cause of electromagnetic interference to electronic equipment systems installed in these spaces.
In prior work, a time-dependent RF energy propagation model has been developed and tested for coupled reverberant spaces in the laboratory [3]. The wireless channel properties investigated included power delay profile, rms time delay spread, coherence bandwidth, average received channel power, signal-strength fading statistics, and maximum field environment.
In this work, the RF energy propagation model is applied to and tested in actual below-deck spaces aboard a ship, the ex-USCG cutter Monhegan. In order to make measurements in a below-deck environment where the coupled spaces are separated by large distances, a fiber optic time-domain measurement technique and experimental setup is utilized. Measurement results indicate that the model can be applied with very good accuracy to such complex spaces and can be useful in providing important communications channel model parameters in the multipath environment.
RF Energy Propagation Model
Model Equations
The time-dependent model for RF energy propagation between coupled complex cavities is presented in [3]. Figure 1 shows the configuration of three coupled spaces aboard the cutter Monhegan. The space volumes are V1 = 135 m3 (engine room), V2 = 20 m3 (communications room), and V3 = 13 m3 (cryptography room).
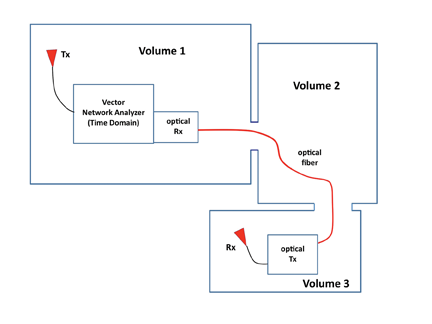
An open double hatch provides the primary coupling between volume 1 and volume 2, and an open door provides the primary coupling between volume 2 and volume 3. Figure 2 provides a view of these spaces.

The spatially-averaged energy densities ui(t) in volume i = 1, 2, 3 are determined from conservation of energy considerations [3]:
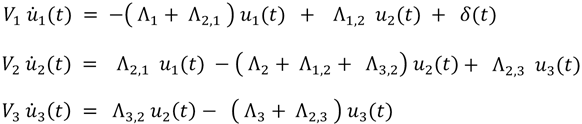
where

and ![]() (t) signifies the time rate of change of the average energy density. δ(t)is an impulse of electromagnetic power delivering 1 J of energy into volume 1 at time t = 0 s. Λi and Λi,j are the energy loss rate coefficients for volume i and for coupling from volume j to volume i , respectively. The losses contributing to the cavity quality factor Qcav include ohmic metal (wall) losses, room content absorption and antenna loading in the space. It does not include the loss due to coupling to an adjacent volume. The loss rate coefficients Λi,j for intercavity coupling are expressed through an averaged transmission cross section ‹σi,j›. Note that reciprocity holds in most cases for the transmission cross sections, so that Λi,j = Λj,i. Vi is the volume of cavity i, ω is radian frequency, and c is the speed of light. The source impulse in (1) can be placed in any of the spaces by moving the term δ(t) to the appropriate equation. The system of coupled first-order differential equations is solved efficiently using the MATLAB math software package.
(t) signifies the time rate of change of the average energy density. δ(t)is an impulse of electromagnetic power delivering 1 J of energy into volume 1 at time t = 0 s. Λi and Λi,j are the energy loss rate coefficients for volume i and for coupling from volume j to volume i , respectively. The losses contributing to the cavity quality factor Qcav include ohmic metal (wall) losses, room content absorption and antenna loading in the space. It does not include the loss due to coupling to an adjacent volume. The loss rate coefficients Λi,j for intercavity coupling are expressed through an averaged transmission cross section ‹σi,j›. Note that reciprocity holds in most cases for the transmission cross sections, so that Λi,j = Λj,i. Vi is the volume of cavity i, ω is radian frequency, and c is the speed of light. The source impulse in (1) can be placed in any of the spaces by moving the term δ(t) to the appropriate equation. The system of coupled first-order differential equations is solved efficiently using the MATLAB math software package.
The model solutions uiδ(t) are the impulse responses for a δ-function excitation that delivers U0 = 1 J energy at time t = 0 s. As such, they can be used as Green’s function kernels in the solution for any time-dependent driving function of power p(t) injected into a cavity.
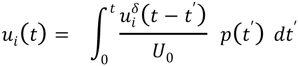
The energy loss rate coefficients are fundamental parameters describing the basic interactions – leakage and ohmic loss – that the reverberant fields undergo. These coefficients are independent of excitation. Two excitations of power p(t) that are common in EMI/EMC testing are the unit step and square pulse functions.
Channel Model Parameters
The mean value of multi-path impulse time delay τ0,i in volume i is given by [4],

The standard deviation of multi-path impulse time delay, i.e., rms delay spread τrms,i , in volume i is given by [4],
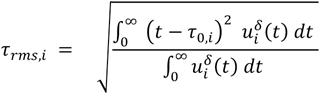
In general, the integrations in (4) and (5) are carried out numerically using the model solutions uiδ(t) from (1).
The average received channel power (RCP) in volume i for a constant transmit power Ptx,1 in volume 1 is given by,

where λ is wavelength and ηRx is the receive antenna efficiency. The steady-state energy density uiss is derived from (3) for p(t) = Ptx,1 as,
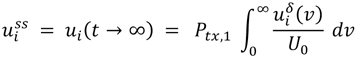
Substituting (7) into (6) yields,

The maximum field environment taken from N samples in volume i has an upper bound given by [5],
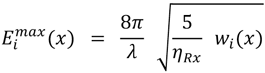
where,

and x is the one-sided confidence level, e.g., x = 0.95. The maximum electric field component amplitude Eimax(x) is predominantly composed of diffuse multipath (non line-of-sight) contributions to the total field in the coupled cavities.
Coupled Cavity Measurements
The frequency-domain transfer function for complex signal amplitude of the wireless channel is provided by the scattering parameter S21n(f) which is commonly measured between two antennas with a vector network analyzer (VNA) [6]. The index n denotes the various stochastic realizations of the channel that occur from mechanical or source stirring in the spaces. Note that the channel here includes the coupled spaces and the transmit/receive antennas. Figure 3 depicts the measured |S21Vol 1→1,2,3|2 frequency responses at the 2.437 GHz wireless band for a single positioning of the transmit and receive antennas between the various spaces. For a given combination of spaces, measurements are taken for a total of n = 15 different transmit antenna locations/orientations (source stirring) and receive antenna locations/orientations (volume sampling). Such measurements are repeated for all the different transmit/receive combinations in the three spaces – a total of 6 combinations since reciprocity holds.
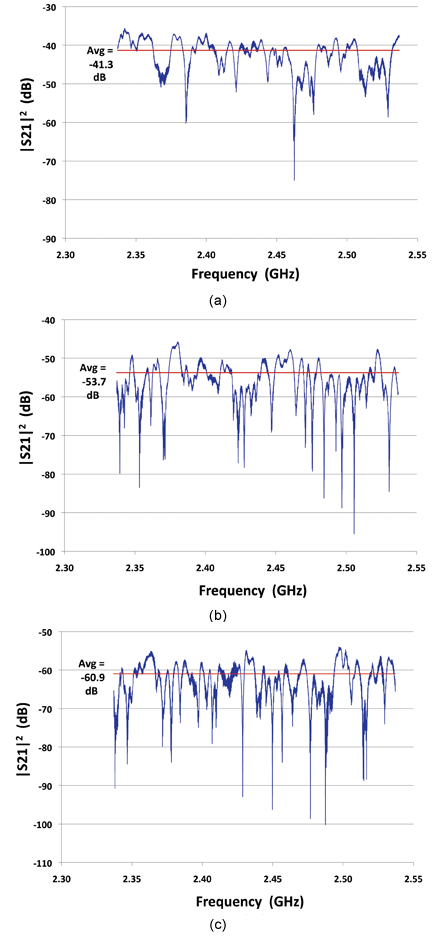
for a single position of transmit and receive antennas. Transmit antenna is located in Volume 1, and receive antenna is located in (a) Volume 1, (b) Volume 2 and (c) Volume 3.
The channel impulse response hn(t) is derived from the frequency-windowed and filtered inverse Fourier transform,
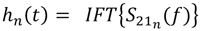
For the 200-MHz bandwidth used in the frequency sweep for S21n(f), the equivalent synthesized input impulse at 2.4 GHz has a nominal 9.8-ns pulse width.
The channel power delay profile PDP(t) is defined as [7],

where the ensemble average ‹ ›n is taken over the n-realizations of the channel. The quantity |hn(t)|2 is most efficiently obtained from a VNA that has a built-in time-domain signal processing module. In terms of the model, the spatially-averaged energy density uiδ(t) in an overmoded complex cavity is proportional to average received power [8]. Since averaging over space is equivalent to averaging over source position (source stirring), the measured power delay profile is related directly to the model through a proportionality constant C as,
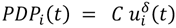
In the below-deck environment, the receive antenna is often a far distance from the VNA, as depicted in Figure 3. To accommodate this remote antenna without sacrificing dynamic range in the measurements, an optical transmit/receive link over a single-mode fiber optic cable is utilized. Since the amplitude and phase of the received signal is important for the inverse Fourier transform in (11), amplitude and phase fidelity in the optical link is critical. The optical link used in this work exhibited excellent fidelity and stability.
Application of Model to Below-Deck Spaces
The measured ensemble-averaged responses and the model solution responses are shown together in Figure 4 at 2.4 GHz for the impulse excitation injected into volume 1 (engine room), volume 2 (comm room), and volume 3 (crypto room). The uncertainty in the ensemble-averaged measurement is indicated by the error bars shown at ±1 σ . Overlaying the model response to the measured response involves adjusting the single set of five energy loss rate coefficients A1 , A2 , A3 , A1,2 and A2,3 so that the shapes and relative magnitudes of the energy density curves u1δ(t), u2δ(t), and u3δ(t) in all three plots (6 independent traces in total) most nearly match the received power curves of the experiment. Because this fitting process does not rely on absolute power values, but on slopes, shapes and relative relationships in the time-dependent received average power curves, we do not require information about the transmit and receive antenna efficiencies. This is a very attractive advantage of the time-domain measurement approach, since antenna efficiency is generally difficult to know with precision in a reverberant environment [9]. The best-fit energy loss rate coefficients for the three coupled spaces at 2.4 GHz are shown in Table 1.
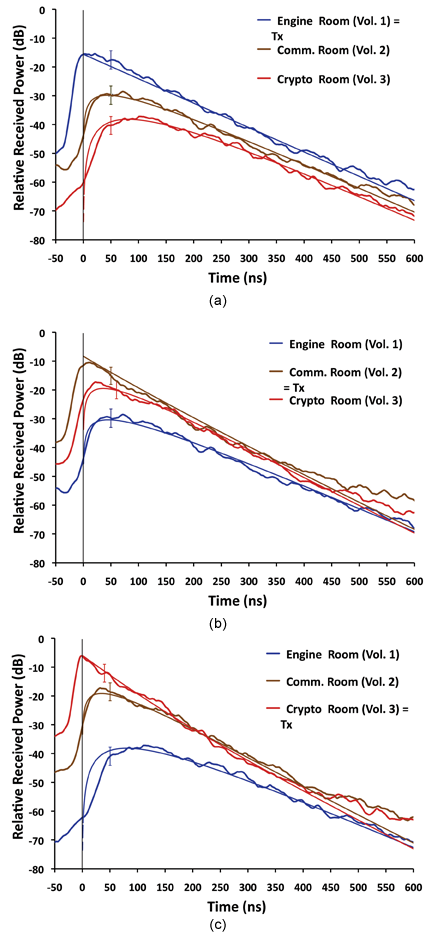

The excellent fit of model solution responses with transient received power measurements is a good validation of the model approach and solution. The model is valid under conditions that (1) each electrically-large reflective cavity in the chain
supports a sufficient number of modes to produce the required statistical field uniformity and (2) the wall scattering time is small compared to the characteristic time constants of energy decay. These requirements impose lower bounds on frequency of operation and on quality factor Q for a given cavity size. At 2.4 GHz, the number of modes excited in all spaces is more than sufficient to produce the statistical field uniformity required of this approach. And while the |S21|2 losses of real below-deck spaces with complex geometry and loading are large, the model approach remains accurate even in these low-Q spaces, with energy decay times on the order of 10-7 sec.
Average time delay, rms time delay spread, and average received channel power normalized to transmit power at 2.4 GHz are calculated by numerical integrations in (4), (5), and (8), respectively, and are presented in Table 2. The normalized received channel powers calculated from (8) compare very well with the measured ‹|S21|2›f values (received power averaged from frequency stirring over 200-MHz bandwidth) shown in Figure 3. To assess the coverage of a wireless transmitter, e.g., a WLAN access point at 2.4 GHz installed in the engine room (volume 1), the average received power RCP3 in the crypto closet (volume 3) is calculated as,


For a transmit power Ptx,1 = 550 mW (27.4 dBm), RCP1 and RCP3 are 34.7 µW (-14.6 dBm) and 0.58 µW (-32.4 dBm), respectively. Based on these example RCP values, we can estimate maximum field levels using (9) and (10). With a sampling value N = 20 per trial and a receive antenna efficiency ηRx = 0.95, the maximum field environments in volumes 1 and 3 are not expected to exceed 6.6 V/m and 0.9 V/m, respectively, at a confidence level x = 0.95.
Conclusion
Energy loss rate coefficients are obtained by overlay of model solutions to time-resolved received power measurements taken aboard a ship. These energy loss rate coefficients are fundamental physical parameters describing the basic energy interactions – leakage and dissipative loss – that the reverberant fields undergo in real below-deck spaces. These coefficients are independent of
the power waveform used to excite the system.
There are two approaches to applying the model to the assessment of RF energy propagation and shielding effects in below-deck compartments and passageways in ships and submarines, and in aircraft cabins and bays. The first approach utilizes a library of energy loss rate coefficients that have been catalogued from measurements in over 100 below-deck spaces and from extensive measurements made in a reverberation chamber of many different types of loading – including large cabling runs, electronic equipment racks, computing stations, palettes of materiel, and personnel. The aggregate energy loss rate coefficient in a given space can be estimated by summing the energy loss rate coefficient of the bare space (dependent on wall material and surface area) and the energy loss rate coefficients of the various types of loading inside the space (dependent on quantity and/or size). Additionally, energy loss rate coefficients for coupling between spaces have been well characterized for apertures, including open hatches and dielectric windows.
The second approach utilizes in-situ VNA measurements of the impulse responses in the actual coupled spaces, with the real operational loading present. Energy loss rate coefficients are then obtained by optimizing the overlay of the model solutions to the actual measurements.
Once the energy loss rate coefficients for the system have been estimated or measured, the full channel model parameters are obtained and are available to aid in making electromagnetic compatibility assessments of the wireless network deployed in the below-deck spaces. The wireless channel properties of interest include power delay profile, rms time delay spread, coherence bandwidth, average received channel power, signal-strength fading statistics, and maximum field environment. ![]()
The authors gratefully acknowledge expert contributions from Robert Richardson, retired NSWC Dahlgren Division, and program support from Anthony Seman, ONR Code 331.
References
- M. Panitz, C. Christopoulos, P. Sewell, D. Hope, J. Dawson, and A. Marvin, “Modelling wireless communication in highly-multipath low-loss environments,” in Proc., 2008 IEEE International Symposium on EMC (Detroit, MI), Aug. 2008, pp. 1-6.
- G. Tait and P. Opperman, “Electromagnetic Compatibility Assessment of Wireless Emissions in Shipboard Spaces,” In Compliance Magazine, pp. 28-35, June 2013.
- G.B. Tait and R.E. Richardson, “Wireless Channel Modeling of Multiply-Connected Reverberant Spaces: Application to Electromagnetic Compatibility Assessment,” IEEE Transactions on Electromagnetic Compatibility, Vol. 55, No. 6, pp. 1320-1327,
Dec. 2013. - A. Goldsmith, Wireless Communications. New York, NY, USA: Cambridge University Press, 2005.
- N. Wellander, O. Lunden, and M. Backstrom, “The maximum value distribution in a reverberation chamber,” in Proc. IEEE Int. Symp. Electromagnetic Compatibility (Montreal, Canada), Aug. 2001, vol. 2, pp. 751-756.
- C.L.Holloway, H.A. Shah, R.J. Pirkl, K.A. Remley, D.A. Hill, and J. Ladbury, “Early time behavior in reverberation chambers and its effect on the relationships between coherence bandwidth, chamber decay time, RMS delay spread, and the chamber buildup time,” IEEE Trans. Electromagnetic Compatibility, vol. 54, no. 4, pp. 714-725, Aug. 2012.
- E. Genender, C.L. Holloway, K.A. Remley, J.M. Ladbury, G. Koepke, and H. Garbe, “Simulating the multipath channel with a reverberation chamber: application to bit error rate measurements,” IEEE Trans. Electromagnetic Compatibility, vol. 52, no. 4, pp. 766-777, Nov. 2010.
- D. A. Hill, Electromagnetic Fields in Cavities: Deterministic and Statistical Theories. New York, NY, USA: Wiley-IEEE Press, 2009.
- J.B. Coder, J.M. Ladbury, and M. Golkowski, “On lower bound antenna efficiency measurements in a reverberation chamber,” in Proc., 2012 IEEE International Symposium on EMC (Pittsburgh, PA), Aug. 2012, pp. 216-221.


