This is the third article of a three-article series devoted to the correlation between the insertion loss and input impedance of passive EMC filters. In the first article, [1], LC and CL filters were discussed, while the second article, [2], was devoted to the π and T filters. This article focuses on LCLC and CLCL, or cascaded LC and CL, filters. Analysis, simulation, and measurement results show that the frequencies at which the insertion losses of these filters are equal are the same frequencies at which the input impedances are equal. These frequencies define the regions where one filter configuration outperforms the other (with respect to the insertion loss). To determine these regions analytically, we compare the input impedances of the two filters.
Input Impedance to the Cascaded LC Filter
The input impedance 
IN to the cascaded LC filter is calculated from the circuit shown in Figure 1.
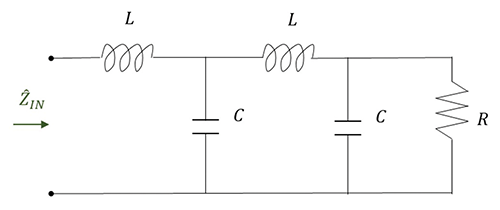
The input impedance of this filter can be obtained by using the input impedance of the π filter [2] and combining it in series with the impedance of an inductor.
(1)
or [3]
(2)
or in terms of the frequency
(3)
The magnitude of the input impedance is
(4)
Input Impedance to the Cascaded CL Filter
The input impedance IN to the cascaded CL filter is calculated from the circuit shown in Figure 2.
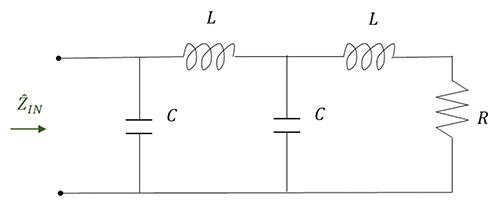
The input impedance of this filter can be obtained by using the input impedance of the T filter [2] and combining it in parallel with the impedance of a capacitor.
(5)
or [3]
(6)
or, in terms of the frequency
(7)
The magnitude of the input impedance is
(8)
Cascaded LC Filter vs. Cascaded CL Filter – Input Impedance – Simulations and Calculations
Let’s look at the input impedances of the two filters. The simulation circuit for this comparison is shown in Figure 3.
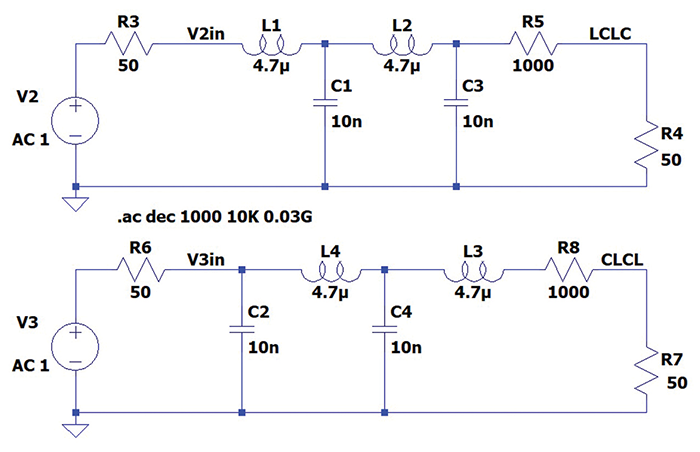
The input impedances of the two filter configurations are shown in Figure 4.
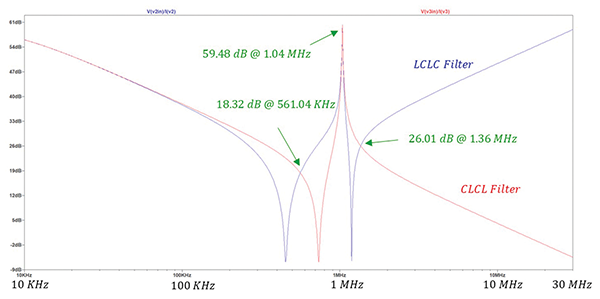
Note that the two input impedances are equal at three frequencies: 561.04 kHz, 1.04 MHz, and 1.36 MHz.
Next, let’s calculate the frequencies at which the input impedances of the two filters are equal. Equating the expressions in equations (4) and (8) produces
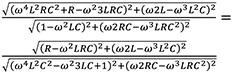(9)
This equation can be solved for ω [3] resulting in
(10a)
(10b)
(10c)
The corresponding frequencies in Hertz are
(11a)
(11b)
(11c)
These results are consistent with the values obtained from the simulation in Figure 4.
Cascaded LC Filter vs. Cascaded CL Filter – Insertion Loss – Simulations and Measurements
Figure 5 shows the simulation circuit used for the comparison of insertion losses.
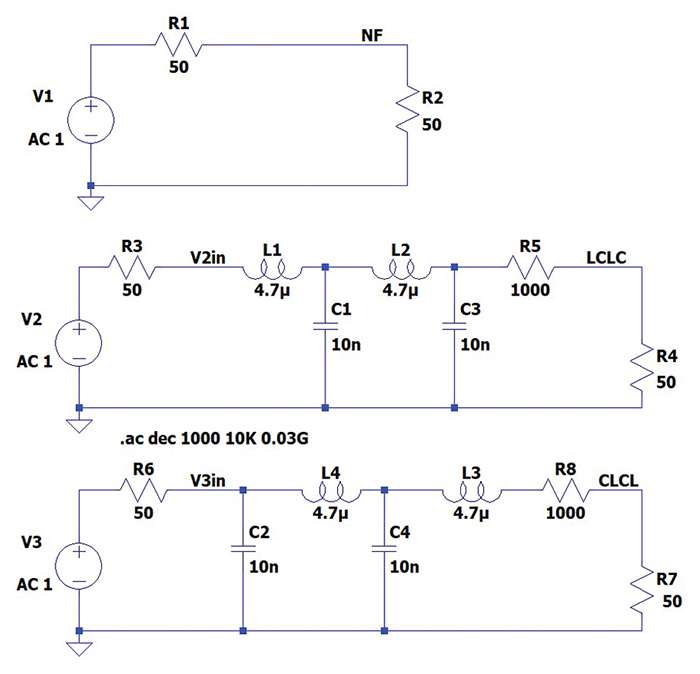
The simulation results are shown in Figure 6.
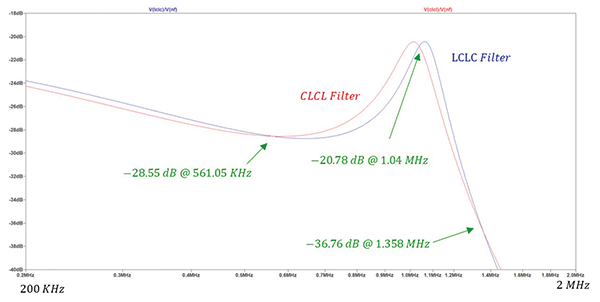
The insertion losses are equal at the frequencies of 561.05 kHz, 1.04 MHz, and 1.358 MHz. These are the same frequencies at which the input impedances of the two filters were equal!
Note that up to the frequency of 561 kHz, the insertion loss of the CLCL filter is larger than that of the LCLC filter. Between the frequencies of 561 kHz and 1.04 MHz, the insertion loss of the LCLC filter is larger. Between the frequencies of 1.04 MHz and 1.36 MHz, the insertion loss of the CLCL filter is larger. Beyond the frequency of 1.36 MHz, the insertion loss of the LCLC filter is again larger.
Once again, [1,2], we have arrived at a very important observation: once the filter components values L and C are chosen, we can determine the frequencies at which the insertion losses of the two filters are equal. These are the frequencies at which the input impedances are equal, given by Equations (11).
To verify the simulation results of the insertion loss, the measurement setup shown in Figure 7 was used.
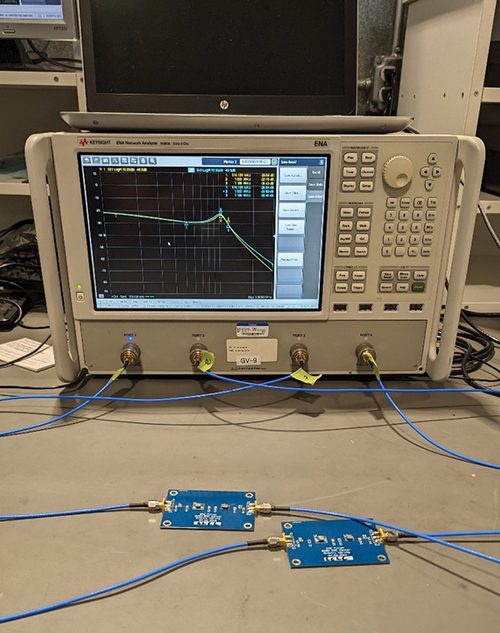
The measurement results are shown in Figure 8.
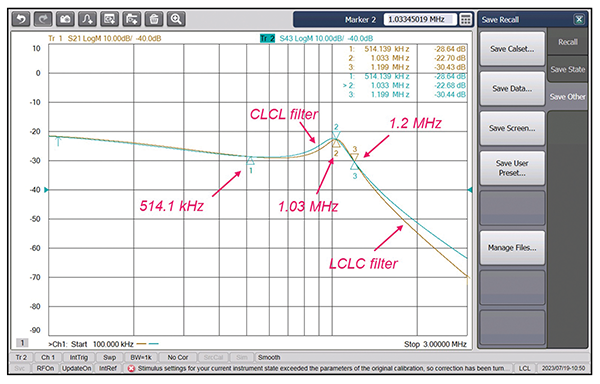
Note that the measurement results agree with the calculated and simulated results.
References
- Bogdan Adamczyk and Jake Timmerman, “Correlation Between Insertion Loss and Input Impedance of EMC Filters – Part 1: LC and CL Filters,” In Compliance Magazine, October 2023.
- Bogdan Adamczyk and Jake Timmerman, “Correlation Between Insertion Loss and Input Impedance of EMC Filters – Part 2: π and T Filters,” In Compliance Magazine, November 2023.
- Bogdan Adamczyk, Principles of Electromagnetic Compatibility: Laboratory Exercises and Lectures, Wiley, 2024.
