Why it’s a problem, characteristics, and simulation.
“My fiber optic equipment is failing in the field. I don’t understand why. It doesn’t have a wired connection to the communications network, and furthermore it has passed testing to all the usual telecommunication standards, including GR-1089 Core [1], ITU-T K.20 [2], K.21 [3], and K.44 [4]”
A previous article (In Compliance, September 2011) discussed why fiber optic equipment might fail even though it didn’t have a wired connection to the communications network [5], as did a similar article by Rust [6]. Now recent field data have identified ground potential rise (GPR) due to lightning as a significant cause of failure of fiber optic communications equipment, e.g. [7], 0.
If GPR is the problem, what are its characteristics?
In [5] the 30,000 A, 3 µsec surge used in the IEEE Guide for Surge Protection of Equipment Connected to AC Power and Communication Circuits [8] was assumed to be the one to use in calculating the effects of a GPR. But is it really? If not, what is the driving waveform for a GPR?
To sort out the general issue of what lightning is, a task force was set up under the auspices of the IEEE PES T&D committee to study the issue. This task force included experts from around the world. The task force wrote a summary of their work, which appeared in the January 2005 issue of the IEEE Transactions on Power Delivery [9]. In essence, they said that no two lightning surges are the same, and that lightning has to be characterized in statistical rather than absolute terms. What they found is that the essential parameters of lightning – amplitude, rise time, fall time, and charge have a log-normal distribution. A log-normal distribution looks like:
 (1)
(1)
Where µ is the median value of the distribution and σ is its standard deviation.
To apply this distribution to lightning, it is necessary to note that lightning surges are of three types: Negative first stroke, positive first stroke, and subsequent [negative] strokes. The character of each is significantly different, and has different implications for protection. The first strokes typically have a relatively slow rise time, long duration, and higher current than subsequent strokes. The first strokes are generally responsible for damage due to heating, due to their high amplitude and long duration. Subsequent strokes are generally responsible for insulation breakdown, due to their fast rise time. The first stroke is most common and about 10% of first strokes have been classified as positive, although there has been some reclassification of positive strokes as upward lightning (see [10]).
Rise Times, Fall Times, and Amplitude
The paper by the task force has tables with the statistical parameters the three stroke types, for use in Equation 1. The parameters for a negative first stroke, excerpted from [9], are shown in Table 1. These values were measured at a tower, or derived from measurements of LEMP [lightning electromagnetic pulse]. This is actually an important point, as different observation points may be the root of some of the disagreement about what the lightning threat is. Anyhow it’s useful to get an idea about what we’re starting with.
| Parameter | Median | Sigma |
| Peak amplitude (Ip), kA | 31.1 | 0.48 |
| 10 – 90 rise time (T10) μsec | 4.5 | 0.58 |
| Fall time (tf) μsec | 77.5 | 0.58 |
Table 1: Statistical parameters of a negative first stroke
Equation 1 is plotted for rise time in Figure 1, just to show what a log-normal distribution looks like. What is of more interest is the cumulative probability curve, which shows the probability being either greater or less than a chosen value. So for example you might want to know what the probability is of a first-stroke amplitude exceeding 50 kA.
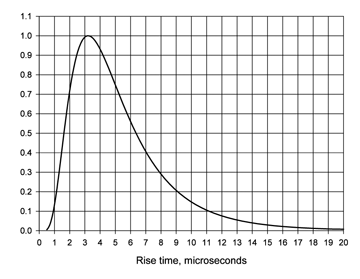
Figure 1: Log-normal distribution of rise time of first negative surge, median = 4.5, standard deviation = 0.58 (Table 1).
The cumulative probability curve is obtained by integrating the probability distribution, which isn’t easy to do. The result is something called an error function. Fortunately, it isn’t necessary to know anything about the error function – you can just look up its values in a table. That has been done for rise time, fall time and amplitude for a negative first stroke, and the results are shown in Figures 2 – 4.

Figure 2: Probability the rise time of first negative surge < chosen value median = 4.5, standard deviation = 0.58 (Table 1)
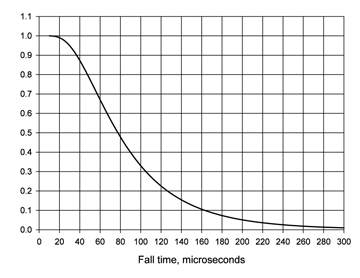
Figure 3: Probability the fall time of first negative surge > chosen value median = 77.5, standard deviation = 0.58 (Table 1)

Figure 4: Probability the amplitude of first negative surge > chosen value median = 31.1, standard deviation = 0.48 (Table 1)
It’s important to note that the 3 parameters of rise time, fall time and amplitude are correlated, so they can’t be chosen independently. Conditional probability analysis can be carried out to answer correlation questions like, “given a 1 µsec rise time, what is the probability that the amplitude will exceed 20 kA?” Conditional probability analysis is complex and is better left for another discussion.
Similar to the negative first stroke, the parameters for a subsequent stroke are shown in Table 2.
| Parameter | Median | Sigma |
| Peak amplitude (Ip), kA | 12.3 | 0.53 |
| 10 – 90 rise time (T10) μsec | 0.6 | 0.92 |
| Fall time (tf) μsec | 30.2 | 0.93 |
Table 2: Statistical parameters of a subsequent stroke
Subsequent strokes are mainly of interest for the high di/dt of their rise time, which combined with circuit inductance can produce enough peak voltage to cause insulation breakdown. The cumulative distribution for a subsequent stroke is shown in Figure 5.
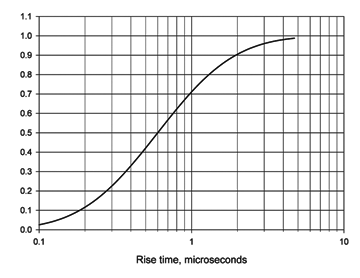
Figure 5: Probability the rise time of subsequent surge < chosen value median = 0.6, standard deviation = 0.92 (Table 2).
Cumulative plots are basically useful for estimating the probability that a chosen design parameter is inadequate. So, for example, suppose we are worried about L(di/dt) spikes, and are assuming a rise time ≥ 3 µs. What is the probability that the rise time is faster than we assumed? From Figure 2 the answer is that about 24% of the surges could rise in less than 3 µs. So if we are designing protection and assume a rise time ≥ 3 µs we may have inadequate protection 24% of the time. Characterizations of this sort are most accurate in the vicinity of the mean and are less accurate out in the tails of the distributions.
Comments
The telecom standards we have today were based on measurements made on wireline systems. As long as the subject is wireline equipment, these standards are appropriate. And indeed wireline equipment tested to these standards has proven reliable in the field. But fiber and wireless systems are different. They are not connected to the external network with wires, so the damage to these systems could be caused by the surges that are quite different from those defined in the existing wireline standards. In fact, there is some evidence that fiber systems that have been successfully tested to the wireline standards have had a significant failure rate in the field. A possibility for this result is that damage was caused by a GPR which had a significantly different waveform from those defined in wireline standards. So the waveforms discussed here are probably more appropriate for testing.
Appropriate Surge Generators
Supposing you wanted to create a standard for testing equipment for resistibility to a GPR surge; or maybe a surge to use for failure analysis testing. Which waveform would you choose? Considering the statistics discussed earlier, there is a wide range to choose from. In the absence of other guidance, the 4.4/ 78 median surge waveshape defined in Table 1 would be a place to start. Now there is a problem – we don’t have a generator that does a 4.5/ 78 waveshape. But maybe an 8/20 combination generator would suffice.
The 8/20 generator waveshape varies with the external resistance connected to it, so that needs to be taken into account. Mick Maytum has calculated the rise time of an 8/20 combination generator as a function of external circuit resistance [11]. These range from 1.59 µs for a 20 ohm load on the generator to 8 µs for a short circuit. We can use these values and values from the probability curve for a negative first stroke to make a plot of the probability that an 8/20 generator would simulate the rise time of a GPR surge vs the external resistance. The result is shown in Figure 6.

Figure 6: Probability that the rise-time of an 8/20 generator approximates the most-likely rise time of a 4.5/78 negative first stroke
What this plot says is that an 8/20 combination wave generator with 5 ohms external resistance is most likely to simulate the rise time of a negative first surge with a median rise time of 4.5 µs. It also says that an 8/20 combination wave generator with an external resistance between about 1 and 19 ohms is at least a 50% as likely to simulate a negative first surge with a median rise time of 4.5 µs as the generator with a 5 ohm external resistance
Similarly, we can use Maytum’s values for fall time to make a plot of the probability that an 8/20 generator would simulate the fall time of a GPR surge vs the external resistance. The result is shown in Figure 7.
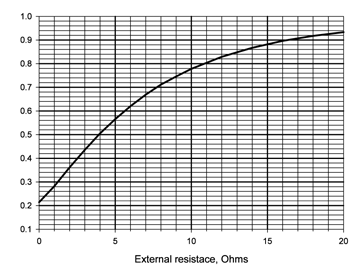
Figure 7: Probability that the fall-time of an 8/20 generator approximates the most likely fall time of a 4.5/78 negative first stroke
What this plot says is that an 8/20 combination wave generator with any external resistance is seldom likely to simulate the most probable fall time of a negative first surge with a median fall time of 78 µs. It also says that an 8/20 combination wave generator with an external resistance greater than 4 ohms has at least a 50% chance to simulate a negative first surge with a median fall time of 78 µs and a most-likely fall time of about 55 µs.
So the conclusion is that an 8/20 combination wave generator produces a reasonable simulation of a first negative stroke GPR. Positive first strokes are pretty rare, so we probably don’t need to worry about those. What about subsequent strokes?
To simulate a subsequent stroke, a generator with a faster rise time than the generally available double-exponential generators is needed. The best candidate appears to be the ring-wave generator defined in IEEE Std C62.41.2-2002™. It has a 0.5 µs rise time and a fall time of about 11 µs. Referring to Figure 8, the ring wave generator with a 0.5 µs rise time has a 76% probability of representing the most likely rise time of a subsequent surge with a median rise time of 0.6 µs.

Figure 8: Log-normal distribution of rise time of a subsequent surge.
Dashed line is ring-wave generator rise time
Similarly, Figure 9 for the fall time of a subsequent surge shows that the ring wave generator has a 99% probability of representing the most likely fall time of a subsequent surge with a median fall time of 30.2 µs.
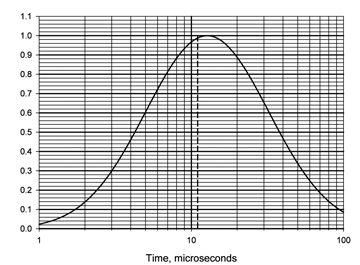
Figure 9: Log-normal distribution of fall time of a subsequent surge.
Dashed line is ring-wave generator fall time
So the conclusion is that a ring-wave generator produces a reasonable simulation of a subsequent stroke GPR.
Conclusions
Both in standards and in the general literature many waveforms have been proposed to simulate the effects of lightning. The point of this discussion has been to select the most suitable ones for evaluating equipment resistibility to damage when a GPR is either the suspected source of the damage, or its effects are to be tested for. With that in mind:
- An 8/20 combination generator can be used to simulate the heating and the insulation breakdown effects of a negative first strike.
- A ring-wave generator can be used to simulate the insulation breakdown effects of a subsequent surge. It could also be used to simulate the heating effects of a subsequent strike, but that is generally not an issue.
![]()
References
- Electromagnetic Compatibility (EMC) and Electrical Safety – Generic Criteria for Network Telecommunications Equipment. Telcordia Technologies, Piscataway, N.J.
- “Resistibility of telecommunication equipment installed in a telecommunications centre to overvoltages and overcurrents”, Recommendation K.20, ITU Telecommunication Standardization Sector (ITU-T), Geneva, Switzerland
- “Resistibility of telecommunication equipment installed in customer premises to overvoltages and overcurrents”, Recommendation K.21, ITU Telecommunication Standardization Sector (ITU-T), Geneva, Switzerland
- “Resistibility tests for telecommunication equipment exposed to overvoltages and overcurrents – Basic Recommendation, Recommendation K.44, ITU Telecommunication Standardization Sector (ITU-T), Geneva, Switzerland
- A. Martin, “Lightning Damage to Equipment without a Metallic Connection to an External Communications Service”, In Compliance Magazine, September, 2011, pp40-47.
- R. Rust, “Do it the Right Way”, OSP Magazine, Aug 9, 2011
- T. Miyazaki, T. Ishii, and S. Okabe, “A Field Study of Lightning Surges Propagating Into Residences”, IEEE Trans. ON EMC, Vol. 52, NO. 4, Nov. 2010
- M. J. Maytum, “Lightning Damage of Home Network Ports”, ATIS PEG Conference 2011 Presentations. Alliance for Telecommunications Industry Solutions (ATIS)www.atis.org
- R. L. Cohen, D. Dorr, J. Funke, C. Jensen and S. F. Waterer. How To Protect Your House and Its Contents From Lightning: IEEE Guide for Surge Protection of Equipment Connected to AC Power and Communication Circuits. 2005, ISBN: 0-7381-4634-X
- “Parameters of Lightning Strokes: A Review”. IEEE Trans. On Power Delivery, Vol 20, No. 1, January 2005.
- B. Glushakow, “10/350 Lightning Test Waveform in Focus”, XI International Symposium on Lightning Protection, 3rd-7th October, 2011Fortaleza, Brazil
- M. J. Maytum, “The 2003 ITU-T Telecommunication Equipment Resistibility Recommendations,” Compliance Engineering 2004 Reference Guide, Figure 5. Combination generator current waveshape variation with external load.
