Using Established Circuit Analysis Techniques and New Capabilities in Modeling/Simulation Tools Can Improve the Understanding Of Battery and Fuel Cell Powered System Performance

Today’s communication, transportation, and power delivery systems all depend on the extensive use of batteries to keep them functioning in a safe and reliable manner. Battery cell technology has its origins in the late 1700s, while fuel cells were not available commercially until the mid‑20^th century. But today’s batteries and fuel cells are an amazing combination of the application of principles of chemistry and electrical engineering.

The standard approach today is that when a battery is the only power source of an electrical system (referred to as the primary power source), analysis techniques are normally applied to characterize the battery as being able to supply constant input voltage to its load. As we have all experienced in our daily lives, constant input voltage conditions do not really exist unless there is an additional power source to maintain the battery’s state of charge.

Unfortunately, this results in a potential divergence of the expected results of electrical and electronic system performance when using the theoretical model compared to what may be experienced in actual real-world applications. For example, when an electrical motor is tested at a constant input voltage, the performance of that motor will vary if the input voltage is changed.

To help engineers better replicate these conditions, this article describes the methods that can be used to increase the correlation of the testing of battery and fuel-cell-powered systems with their actual applications.

The Importance of Test Design

Linear circuit analysis (LCA) is typically a standard methodology used in electrical circuit design, development, and testing for electrical systems. With recent developments and the widespread global production of electric propulsion methods for transportation systems, a comprehensive test design approach that complements LCA can be valuable.

There are many benefits of having up-front test data that has a high correlation to a system’s actual performance. These new methods can be based on the fundamental principles of the conservation of energy when a battery is used as a system’s primary power source. It turns out that, instead of a battery having an unchanging constant energy delivery rate (with a constant current and voltage depending only on the load’s power demand), a battery’s behavior will be impacted due to the type of load to which it is supplying energy, which will then change the characteristics of a battery’s discharge conditions.

There are two types of electrical loads, passive and non-passive. If a load is a passive load, there is no power required. A non-passive load is an electro‑mechanical load like a motor connected to a pump or fan. The pump or fan has power that is required from the mechanical domain, and the motor must provide the required mechanical power. The mechanical power must come from the electrical domain. Note the electro-mechanical coupling could be direct or indirect LCA as an applicable methodology.

When a battery is delivering energy to non-passive loads, the power demand must be satisfied, such as with a motor driving a pump. With this insight, battery modeling can be designed to also provide test results that have a higher correlation with other types of electrical components, such as common power electronics, such as capacitors and inductors.

Both batteries and fuel cells are electro-chemical systems, but a battery is an energy storage device, while a fuel cell is an on-demand power supply that provides power as long as the fuel cell is supplied with hydrogen and oxygen. The fuel cell is considered a current-controlled voltage source (CCVS) and its output voltage is a function of its output current.

As a result, batteries and fuel cells are electro-chemical components that convert chemical energy into electricity and heat. Their energy is stored chemically, and their characteristics will be different from other electrical energy storage devices.

Battery Characterization

A battery is typically characterized by a constant current discharge. What is actually happening is that, as the discharge current increases, there will be an energy loss within the battery itself, as shown in Figure 1.

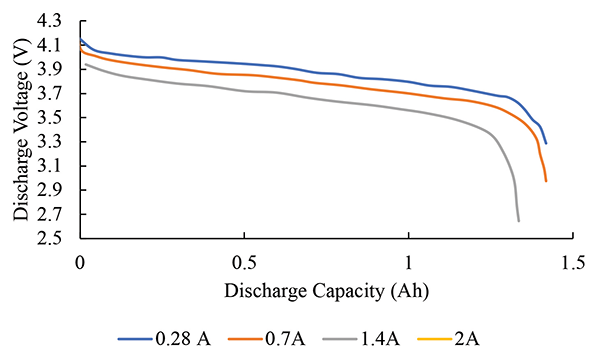
Based on the behavior shown in Figure 1, a battery is sometimes believed to have an unchanging effective resistance. However, the battery discharge voltage will change based on its state of charge as well as the current it is delivering. The consequence is that, as energy is extracted from a battery, the amount of stored charge in the battery decreases.

The SIMULINK model in Figure 2 shows a battery model that correlates discharge voltage, current, resistance, and the battery’s state of charge (SOC).

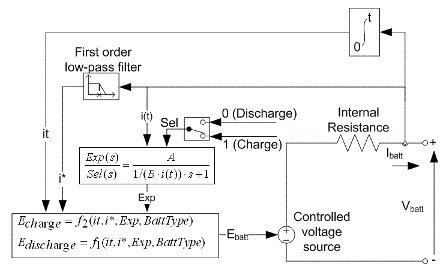
What the model in Figure 2 (with the coefficients that have been obtained from experimental data) shows is that a generic battery model can be used that will incorporate the ability to determine the battery charge, as well as the computation of discharge voltage and resistance.

As we see in Figure 3, the battery is considered a controlled voltage source, where its open circuit voltage will reduce as the state of charge decreases. As a result of the SOC decreasing, the discharge voltage will also decrease.

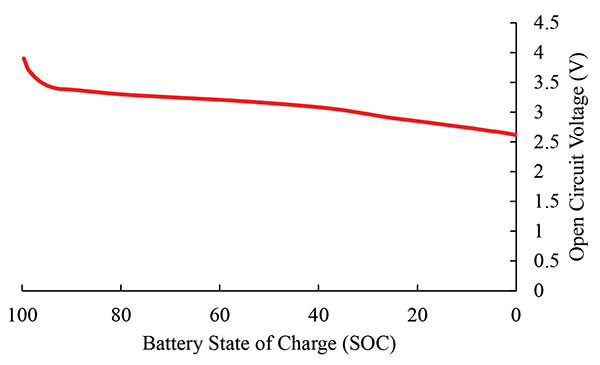
This information then gives us the ability to create a generic battery model that is dependent on certain points in the discharge curve, as shown in Figure 4. The points can be used to determine varying battery SOC and will then yield a quantifiable battery discharge function.

Evaluating Battery Power Source Behavior

Does the battery behave the way it is characterized or does it behave as a constant power source? This could be answered depending on whether the load is passive or non-passive.

Since a battery is a component that stores its energy chemically, it can have two types of discharge characteristics, either constant current or constant power. In Figure 5, we see that, during constant current discharge, the battery discharge voltage is also continuously decreasing. As a result, the power delivered by the battery will also decrease due to the falling voltage.

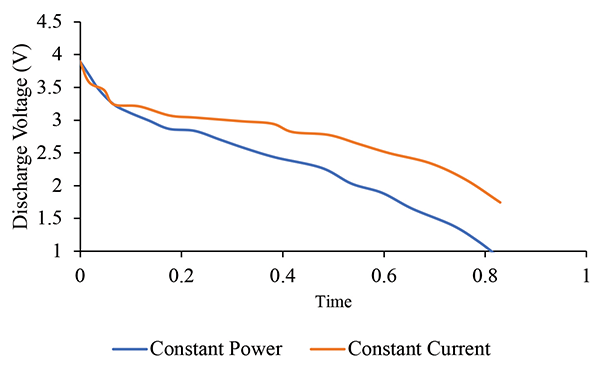
With constant power discharge, the battery discharge voltage decreases faster than the constant current discharge. In this case, the battery discharge power will meet the demands of the load.

In constant current discharge, the discharge voltage decreases along with the SOC. If the electrical is passive, then it can accept a constant current discharge. However, if the load is non-passive, it will require constant power discharge.

In Figure 6, we see how the battery discharge current is influenced by constant current and constant power discharge.

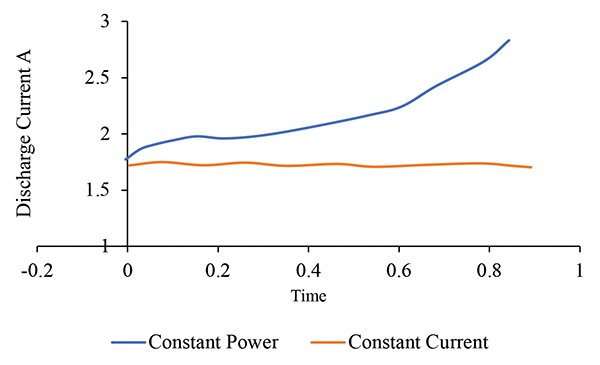
During constant current discharge, the current remains constant and does not change with time. In the case of constant power discharge, the current is low initially when the voltage is high and the current increases as the battery discharge voltage decreases to maintain the power. Note that during constant power, the power discharge is constant at the expense of decreasing voltage and increasing current. Also, the capacity of the battery will decrease more rapidly during constant power discharge and must be sustained by integrating the current.

In Figure 7, we see how power delivery is impacted by battery discharge. In the case of constant current, the battery power delivery is decreasing due to the fall in battery voltage. In the case of constant power, the discharge power remains constant, but voltage and current are also continuously changing. As the voltage decreases, the current increases, which results in the rapid loss of SOC and increased heat generation.

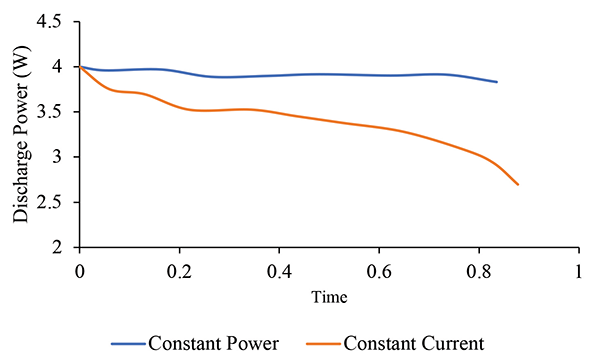
Unlike a fuel cell that is capable of providing a constant voltage and current, a battery is limited in that it can provide constant power but not constant voltage.

Evaluating System Source and Load

The constant current discharge and constant power discharge may impact the applicability of LCA and need to be assessed to confirm whether that is applicable or not. This is answered by looking at the characteristics of the system source, load, or both.

This theory can also be applied to a DC motor and a resistor, inductor, and capacitor (RLC) circuit. The circuit model of the DC motor is shown in Figure 8.

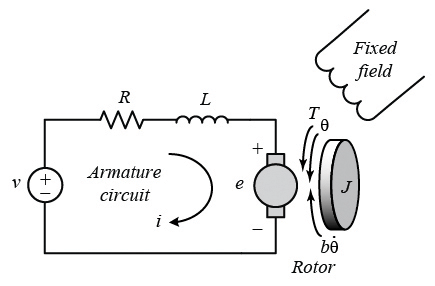
An electric motor can be mathematically represented by the use of two differential equations, as shown in Equation 1 and Equation 2:

  Eq. 1

  Eq. 2

In the current model, the voltage of the source is known and kept constant. If a battery is discharging constant power, the voltage and current will not remain constant. Therefore, we need to reexamine the motor model with variable input voltage, starting with the conservation of energy in its raw form, as shown in Equation 3:

  Eq. 3

Note that the differential equation is not homogenous, and current (I_b) only appears in three terms. The required power comes from the mechanical domain. To simplify the process, we divide the equation by I_b, as shown in Equation 4:

  Eq. 4

The resistor voltage can be further simplified through Ohm’s Law, as shown in Equation 5:

 Eq. 5

In the case of the electric motor, the load will be non-passive due to the motor having to provide power to satisfy the mechanical load. As the current changes, the required voltage will also change. As the voltage decreases, the required current will increase, and the increasing current will also reduce the battery state of charge.

The last term of the equation contains power and current. The required power is known, but current and voltage are changing. Therefore, we cannot solve the equation for voltage and current at the same time. First, we must solve for the current. Then, we can solve for the voltage.

To further complicate the issue, the efficiency of electronics changes with input voltage is shown in Figure 9 and Figure 10.

With the change in the efficiency of electronics, the input voltage and current need to be known to compute the power so that, as input voltage drops, the input current will increase along with the power needs. This makes the power required further dependent on voltage and current.

Equation 5 and Equations 1 and 2 are not the same, but Equation 5 can be simplified by using Equations 1 and 2 and assuming a constant voltage. In the case of Equation 5, LCA cannot be used. But the insights derived by the current in the denominator can help explain inrush current.

The new equation is non-linear and non-homogenous and would give a different solution to the existing model.

Examining a Battery in an RLC Circuit

The next step involves examining a battery in an RLC circuit. The current equation obtained from Kirchoff’s Voltage Law (KVL) is shown in Equation 6:

 Eq. 6

The conservation of energy is applied to the RLC circuit, as shown in Equation 7:

Eq. 7

Note the current is in each term, and the equation is homogenous and linear. The current can be factored out of each of the terms as shown in Equation 8:

Eq. 8

The equations for voltage and current for capacitors, resistors, and inductors can be substituted into Equation 8, resulting in Equation 9:

Eq. 9

Note that the conservation of energy shown in Equation 9 is the same as in Equation 6. Therefore, linear circuit analysis can be used, which is the reason we propose the use of the electrical matrix since it shows the typical approach for all source and load characteristics (see Figure 11).

Figure 11: Typical use cases of linear circuit analysis

It can be seen that LCA is a special case of the conservation of energy.

The next step involves examining where we are with our current circuit analysis, as shown in Figure 11. Based on our dynamic motor modeling with a battery as the main power source, we are proposing adding an additional tool to the toolbox and limiting the use case of LCA. The new proposed matrix is shown in Figure 12.

Figure 12: Proposed change for applicability of linear circuit analysis

Like the battery, the other source of electro-chemical energy is the fuel cell. Unlike a battery, a fuel cell is an open system in which hydrogen and oxygen are delivered to produce voltage and current. The next question that comes up is where the fuel cell fits within the electrical matrix and whether it will follow the battery or go elsewhere.

One of the differences of the fuel cell is that it provides power-on-demand in which its discharge voltage is a function of current. The fuel cell is considered a steady-state load. A steady-state load can provide constant current and constant voltage. A fuel cell can provide a constant voltage and current as long as hydrogen and oxygen are provided to the fuel cell. A sample polarization curve of a fuel cell is shown in Figure 13.

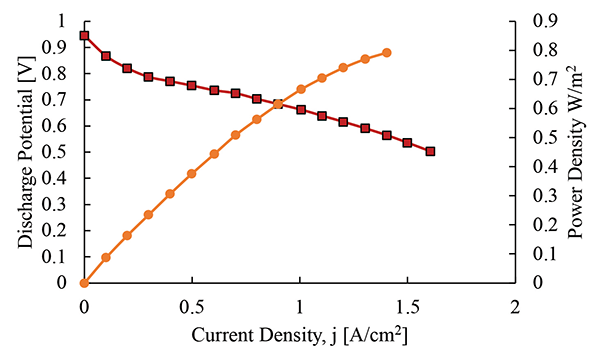
Note that the voltage drops as more current is drawn, but the system can reach a steady-state solution. In this case, Equation 4 can be solved since the power source is considered a current-controlled voltage source:

Eq. 10

If Equation 10 is substituted for Equation 4, the differential equation will only contain current as shown in Equation 11:

Eq. 11

As a result, we can solve for the current and then obtain the voltage. The battery is considered a dynamic source since it cannot provide constant power with constant voltage and constant current.

Defining Passive and Non-Passive Load

The next point involves defining a passive and non‑passive load. The main components integral to passive loads are capacitors, resistors, and inductors. In each of these cases, a voltage-current relationship can be applied to the electrical power equation, as shown in Equations 12, 13, and 14.

The first case that is examined is the capacitor. The electrical power is computed by the voltage and current, as shown in Equation 12:

Eq. 12

In the capacitor, there is a relationship between current and the derivative of voltage with respect to time, as shown in Equation 13:

Eq. 13

By combining Equation 12 and Equation 13, a relationship between voltage and power can be obtained. This function is continuous everywhere:

Eq. 14

The next component that falls into the passive load is the resistor. The resistor has a voltage and current relationship, as shown in Equation 15:

Eq. 15

If Equation 15 is combined with Equation 12, two equations can be obtained for the resistor power, as shown in Equation 16:

Eq. 16

Like the capacitor, the power can be related to either voltage or current and is continuous everywhere.

The last component is the inductor, and the voltage and current relationship for this component is shown in Equation 17:

Eq. 17

The voltage relationship of Equation 17 can be placed into Equation 12 to obtain Equation 18:

Eq. 18

Like the capacitor and resistor, the inductor power can be expressed in terms of one variable and is continuous everywhere.

A non-passive load involves loads in which power requirements must be satisfied, and the voltage and current respond to the power needs. Power is known in the case of electrically generated power. But voltage and current are not known in cases in which the battery is the primary load.

If KVL is applied, the power is divided by the current to convert into the voltage domain, as shown in Equation 19:

Eq. 19

In this case, the voltage function from Equation 19 is not continuous everywhere. So as the current increases, the required voltage decreases until it hits the asymptote. The element introduced is a power-based element in which the element requires constant power.

The proposal for electrical circuit analysis involves the transition from the matrix shown in Figure 11 to the matrix shown in Figure 12. To proceed, the load and the source need to be examined to determine whether linear circuit analysis is applicable. For instance, in a case where the source can provide a constant voltage and current, such as with a fuel cell or a power supply, the input voltage to the system will be constant. In this case, we can solve for the voltage and current at the same time and LCA can be used.

The next step of the process involves examining the sources to see how they will impact the proposed electrical matrix. In addition, all four cases will be tested to validate the theory.

Conclusion

Today’s electrical and electronic systems depend on portable sources of energy to be able to meet the demands (and expectations) of customers and users of those systems. LCA, as used in our circuit analyses, identifies issues with the broad applicability of the model due to interactions between the power source the load and has been shown to be valid in only three of the four usage cases we evaluated. Accordingly, to meet the challenges of creating systems with the highest value, lowest mass batteries and fuel cells, a new approach can be used, one that involves using the conservation of energy to develop a relationship between voltage and current required by both passive and non-passive loads.

The raw form of the conservation of energy can use LCA when passive elements are present. But there are limits to the use of LCA, and a new tool is needed to solve new problems. Our hope is that new insights resulting from our research will help size batteries for existing needs, size electronics components to minimize conduction and switching losses, and improve electronic efficiency.

In addition, battery evaluation needs to include the connection between the source and the load. For instance, a motor used in a battery electric vehicle should be tested with a variable input versus a constant input load to get an accurate representation of how the motor and electronics will actually behave in the real world.

References

1. Handbook of Batteries, Third Edition, David Linden, Thomas Reddy.
2. https://www.mathworks.com/help/sps/powersys/ref/battery.html
3. https://ctms.engin.umich.edu/CTMS/index.php?example=MotorSpeed&section=SystemModeling
4. https://www.ti.com/lit/ds/symlink/tps61045.pdf
5. Fuel Cell Fundamentals, Second Edition, Ryan O’Hayre, Suk Won Cha, Whitney Colella, Fritz B. Prinz.