Modeling the RF Switch Front End Module ESD Protection

Due to the proliferation of wireless applications ranging from cellular and automobile communication systems to the Internet of Things, RF switching and tuning solutions continue to provide challenges for both device and system-level ESD protection. Most of the RF switching that is needed is built in the silicon-on-insulator (SOI) process technology, as shown in Figure 1. Thin-film SOI provides the substrate that enables both the high RF performance and the transistor isolation needed for high-power RF signal processing. One of the intrinsic advantages of the SOI RF switch is the self-protection it can provide for device-level ESD threats [1]. Furthermore, when properly co-designed with the system-level ESD protection, the SOI switch can contribute to the protection of the total antenna system.

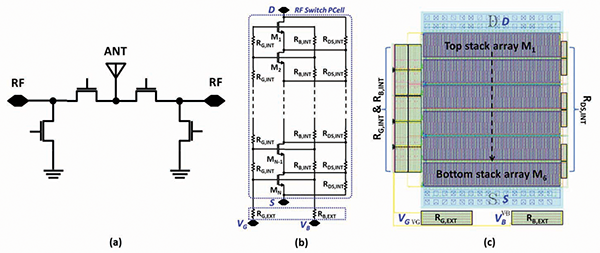
Understanding this self-protection mechanism and then successfully modeling it is critical for the SOI switch circuit designer. The turn-on mechanism for the switch in an ESD event is actually the synergy of two mechanisms [2,3]. The large gate resistance (R_G) and the gate capacitance (C_GD) result in an RC time constant that is sufficiently large that, when the ESD pulse strikes the switch, the switch transistor gate couples up, turning the transistor array on. Assisted by this channel current and initiated by the avalanche breakdown at the transistor drain, the parasitic bipolar turns on, providing the secondary ESD protection mechanism. The TLP plot of the response of a single stack switch to the ESD pulse, as well as the dual protection mechanism, is shown in Figure 2. In Figure 2(a), the gate bias during the TLP testing was 1V.

Early attempts to model the ESD self-protection of the SOI switch utilized TLP data and curve-fitting polynomial equations. The curve fit equation in the previous approaches contained parameters for stack width W_T and number N_S and can identify the failure current I_FAIL for the switch. However, there were severe limitations with this approach. First, these were not scalable models for transistor gate length. Additionally, it could not predict the effect of R_G on the gate-coupling mechanism. Since the ESD self-protection of the switch is initiated by the gate-couple effect, which is determined by the (R_G*C_GD) RC time constant, the inability to properly simulate this coupling severely limits its usefulness.

To address the deficiencies of the curve-fitting model, a behavioral model that comprehends the dual mechanism of the switch turn-on in an ESD event has been proposed [3,4]. Figure 3 graphically shows the behavioral model of the NMOS in a multiple-stack RF switch. This model contains two parts connected in parallel: the standard FET model for NMOS channel conduction and the ESD model for the parasitic bipolar turn-on. While this is an oversimplification of the behavior observed in Figure 2(a), the ESD model is considered an ideal switch in series with a resistor. The switch turns on at the parasitic bipolar trigger voltage (V_TR) to shunt the ESD current with a fixed on-resistance (R_ON). The values of the two ESD model parameters can be extracted from the TLP measurement data of multiple-stack SOI RF switches.

Figure 4 shows the time‑domain voltage and current waveforms of a 16-stack RF switch from the TLP measurement and the corresponding transient simulations for stress voltages of 5V to 50V. As is observed in Figure 4, the simulation and measurement match quite well for TLP voltages below 20 V. However, for stress voltages above 20V, the simulation and measured data begin to diverge. This divergence is due to the oversimplification of the ESD model for bipolar conduction. To model the ESD behavior more accurately in the high current regime, the simple turn-on of an ideal switch with a fixed on‑resistance would need to be replaced with the more complicated model of the turn-on of the NMOS parasitic bipolar transistor. This is one of the ongoing efforts in the refinement of the ESD modeling of the SOI switch response to the ESD event.

One of the more important features of a useful ESD model is its ability to predict I_FAIL. Indeed, I_FAIL is often more important than failure voltage V_FAIL since I_FAIL can be used to predict the HBM failure current level. The simple ESD behavioral model can predict I_FAIL by monitoring the voltage at which the parasitic bipolar is triggered. If the gate coupling is not sufficiently strong, the voltage of the transistor will rise above a failure level prior to the onset of the bipolar conduction. This failure voltage is determined empirically from TLP data. Exceeding this failure voltage indicates failure of the switch due to the R_G*C_GD time constant being too short. For a switch with a sufficiently large time constant, I_FAIL does not occur until one of the transistor arrays reaches the failure voltage well after the parasitic bipolar turns on.

References

1. A. Tombak, M. S. Carroll, D. C. Kerr, J.‑B. Pierres, and E. Spears, “Design of high-order switches for multimode applications on a silicon-on-insulator technology,” IEEE Transactions on Microwave Theory and Techniques., vol. 61, no. 10, pp. 3639-3649, October 2013.
2. J. Liu, N. Carels, and N. Peachey, “Characterization and Analysis of RF Switches in SOI Technology for ESD Protection,” 2022 IEEE International Reliability Physics Symposium (IRPS), Dallas, TX, USA, 2022, pp. P13-1-P13-5.
3. J. Liu and N. Peachey, “A Behavioral Model for ESD Self-Protection RF Switches in the SOI CMOS Technology,” 2022 International EOS/ESD Symposium on Design and System (IEDS), Chengdu, China, 2022, pp. 1-8.
4. M. Di, A. Nath, M. Miao, X. X. Lu, L. Lin, and R. Gauthier, “Electrostatic Discharge Switch Simulation Enablement in RF SOI Technology,” 2021 IEEE International Symposium on the Physical and Failure Analysis of Integrated Circuits (IPFA), Singapore, 2021, pp. 1-5.