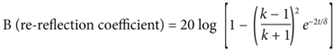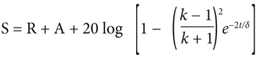In this article, we analyze the shielding effectiveness equations (SE = R + A + B) as defined by Ott, Schnelkunoff, White, and Frederick. The analysis consists of deriving the values of R and A, and evaluating and comparing the values of R, A and B with test results obtained by Al Broaddus and George Kunkel in their paper entitled “Shielding Effectiveness Tests of Aluminizing Mylar.” The analysis and test data presented clearly demonstrate that the equations have been misinterpreted by Schelkunoff and others, and that there is no reflected loss inside a shielding barrier. The contribution to shielding theory by Schelkunoff is also evaluated. An analysis of circuit theory versus wave theory is performed, and the results conclude that wave theory does not represent the actual phenomena associated with a conducted wave on a transmission line, and that wave theory is only a theory.
In this article, we analyze the shielding effectiveness equations (SE = R + A + B) as defined by Ott, Schnelkunoff, White, and Frederick. The analysis consists of deriving the values of R and A, and evaluating and comparing the values of R, A and B with test results obtained by Al Broaddus and George Kunkel in their paper entitled “Shielding Effectiveness Tests of Aluminizing Mylar.” The analysis and test data presented clearly demonstrate that the equations have been misinterpreted by Schelkunoff and others, and that there is no reflected loss inside a shielding barrier. The contribution to shielding theory by Schelkunoff is also evaluated. An analysis of circuit theory versus wave theory is performed, and the results conclude that wave theory does not represent the actual phenomena associated with a conducted wave on a transmission line, and that wave theory is only a theory.
Shielding Effectiveness Equations
Most of the literature dealing with the shielding theory of electromagnetic (EM) waves defines the level of attenuation of the wave through a barrier by the use of shielding effectiveness equations. These equations are:
SE (shielding effectiveness) = R + A + B
Where:
A (absorption loss) = 20 log e-t/δ= 8.686 t/δ
Table 1 illustrates the analysis results using the shielding effectiveness equations (as given in the Sidebar “Shielding Effectiveness Equations”) on the test conditions used by Broaddus and Kunkel. The test results obtained by Broaddus and Kunkel (and shielding effectiveness analysis) are based on the following test conditions: 1) the test barrier has a resistance of 1.4 ohms (impedance of 2.0 ohms); 2) the EM wave sources are a high impedance (electric dipole) antenna and a low impedance (magnetic dipole) antenna 20 centimeters from the barrier; and 3) the frequency range is between 100 kHz and 10 MHz.
Comparing the results of the analysis with the test results (as illustrated in Figures 1 and 2 and Table 1) yields significant insight into the meaning and value of the equations.
The reflective loss “R” is derived from transmission lines as obtained using the equations associated with “wave theory.” It is assumed that the reflection coefficient (R) using the wave theory equation on a transmission line is identical to that of when a radiated wave is reflected from a shielded barrier, where the loss is equally the same for the E and H fields. Figures 1 and 2 compare the results obtained using the “SE” equations with the E field attenuation obtained by Broaddus and Kunkel. No loss in the H field was detected during the test.
The term “absorption loss” implies a power loss (or an I2 R loss as defined in our high school physics classes). It is actually an attenuation factor. When an EM wave is impinged on a shielding barrier, current (surface current density -Js) is coupled to the barrier. This current generates an H field at right angles to the direction of the current. The H field in turn creates a back EMF (voltage) which forces the current flowing in the barrier to flow close to the incident surface of the barrier. This phenomenon is classified as “skin effect” where the average depth of the current flowing on the surface of an infinitely thick (greater than an extinction depth or 2Πδ meters) is one skin depth where δ is one skin depth.
The “re-reflective coefficient” is applicable when the thickness of the barrier is “thin” (less than 2Πδ). In the literature on shielding, this function is to be applied due to the wave bouncing back and forth inside the barrier. The equation is actually a correction factor for assumptions made in applying the reflection loss equation. These assumptions are:
- The wave impedance Zw is greater than the barrier impedance Zb. The equation for “R” yields a reflective loss when Zw < Zb. As illustrated in Figure 1 and Table 1, there is not a loss of shielding under these conditions. The equation for “B” is a correction factor when Zw is less the Zb (as is the case at 100kHz using the low impedance source).
-
The thickness of the barrier is greater than 2Πδ meters. The equation for the impedance of the barrier (consistent with shielding effectiveness theory) is:

When this equation is applied to the test conditions used by Broaddus and Kunkel, the impedance of the 2.0 ohm barrier results in impedance of .0001, .0005 and .0015 ohms for 100 kHz, 1MHz and 10 MHz respectively. The actual impedance for a barrier of any thickness is:
Using this equation, the impedance is 2.0 ohms for all three frequencies. The “B” equation containing (1 − e−2t/δ) is used as a correction factor when the thickness “t” is less than 2Πδ (see Table 1).
| Antenna Source | Zw | Zb | K | δ | e-2t/δ | k-1 2 k+1 |
R dB | B dB | A dB | SE dB |
| @ 100 kHz | ||||||||||
| High Z | 9×105 | .0001 | 6×109 | .0003 | .9998 | 1.0000 | 183.6 | -76.4 | 0.0 | 107 |
| Low Z | .158 | .0001 | 1058 | .0003 | .9998 | .9962 | 48.4 | -48.1 | 0.0 | 0 |
| @ 1 MHz | ||||||||||
| High Z | 90,000 | .0005 | 190×106 | .0001 | .9995 | 1.0000 | 153.6 | -66.4 | 0.0 | 87 |
| Low Z | 1.0000 | .0005 | 2120 | .0001 | .9995 | .9981 | 54.5 | -52.5 | 0.0 | 2 |
| @ 10 MHz | ||||||||||
| High Z | 9000 | .0015 | 6.03×106 | 2.67×105 | .9905 | 1.0000 | 123.6 | -56.4 | 0.0 | 67 |
| Low Z | 15.79 | .0015 | 16×103 | 2.67×105 | .9905 | .9996 | 68.5 | -54.5 | 0.0 | 14 |
Table 1: Shielding Effectiveness Analysis of Test Conditions used by Broaddus and Kunkel in their Presentation at the 1992 EMC Symposium.
Most of the literature on the shielding of EM waves states that the attenuation of the E and H fields through a barrier is equal. This is justified because the reflection loss “R” equation provides for a loss when Zw < Zb. The impedance inside a barrier is less than the 377 ohm impedance of free space. However, we know from Table 1 that the shielding equations predict zero shielding under these conditions. As a result there is no reflected loss inside the barrier. Any H field attenuation is the result of skin effect or the absorption “A” equation.
Schelkunoff’s Contribution to Shielding Theory
Sergei Alexander (S.A.) Schelkunoff is credited with providing the electrical engineering community with the theory of shielding electromagnetic waves. In his book Electromagnetic Waves published in 1943, he provided the
engineering community with the presently accepted shielding effectiveness equations, i.e.:
Where:
A = 8.686 t/δ
& k = Zwave/Zbarrier
Along with the equations, he also provided us with an example for which he developed the values of R and A. He also provided the following interpretation of the reflection loss equation “R:” “The wave is partially reflected at the outer surface of the shield and then partially re-reflected at the inner surface.”
The reflection loss “R” is derived using “wave theory” as applied to conducted transmission lines. Schelkunoff believed that wave theory represented a physical representation of a wave on a transmission line. He also believed in a direct relationship to the reflective loss in a transmission line as predicted by wave theory and the reflective loss associated with a radiated wave striking a shielding barrier. The analogous relationships between the reflective waves are as follows:
- The Impedance (E/H) of a radiated wave striking a barrier is analogous to the characteristic impedance (Zo) of a transmission line.
- The reflected E field of a radiated wave (when Zw > Zb) striking a shielding barrier is analogous to the reflected voltage of a transmission line when Zo > ZL.
- The re-reflected wave at the inner surface of a shielding barrier is an H field and is analogous to the reflected current loss of a transmission line when Zo < ZL.
The third analogy of the H field being analogous to the reflected current is the justification for the wave being “partially re-reflected at the inner surface.” As is illustrated in Figure 1 and Table 1, there is no predicted or measured shielding effectiveness (using the SE equations) when Zw < Zb. Therefore, the argument for a reflected wave inside the barrier is not valid, and does not exist.
Summary
The hypothesis upon which the shielding effectiveness, and accepted shielding theory, are based is: 1) that wave theory represents the actual physical phenomena associated with a transmission line; and 2) the reflective coefficients as predicted using wave theory on a transmission line are identical to that of a radiated wave striking a shielding barrier. This hypothesis is incorrect. As illustrated in the Sidebar to this article, “Circuit Theory vs. Wave Theory,” wave theory does not produce accurate circuit results when the load and source impedance are not resistive. The reflected E and H field form a radiated wave striking a barrier cannot be predicted using wave theory, as there is no H reflected wave when the wave impedance is less than the barrier impedance (Zw < Zb).
|
Shielding Effectiveness Equations SE = R + A + B (dB) Where: A = 8.686 αd Absorption Loss (dB)
Z wave≈ – j 377 λ / 2 π r, (r < λ / 2 π) High Impedance Source ≈ j 377 (2 π r / λ), (r < λ / 2 π) Low Impedance Source ≈ 377, ( r ≥ λ / 2πr ) All Sources d = Thickness of Barrier (meters) r = Distance from Source to Barrier (meters) ω = 2πf µ = Absolute Permeability of Barrier (H/m) µ = 4 π x 10-7 σ = Absolute Conductivity of Barrier (mhos/m) σ copper = 5.82 x 107 σ aluminum = 3.55 x 107 λ = c/f = 3 x 108 / f (meters) Extracted from “Handbook of RFI, Volume 3”, |
|
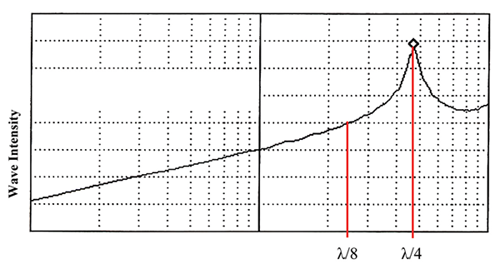
Circuit Theory vs. Wave Theory In the mid-1800s two principal methods of solving electrical circuit problems were proposed. They were wave theory and circuit theory as formulated by Gustav R. Kirchoff. Kirchoff’s laws and subsequent equations proved to be easier to understand and use, and considerably more applicable. Wave theory was discarded but not forgotten. A cursory look at wave theory is taught in nearly all graduate-level courses on electromagnetic theory. This consists of informing the student that, when the load impedance of a transmission line varies from that of the characteristic impedance of the transmission line, the conducted wave is reflected. The basic laws and equations governing the reflection are provided. Detailed analysis as contained below is not performed. As a result most electrical engineers refer to the reflection of conducted waves. We prefer to use the logic and equations described by Walter C. Johnson in his book Transmission Lines and Networks. Using Johnson’s laws and equations, the load impedance (as viewed from the source) varies as a function of the length of the line versus the wave length of the frequency of concern (as illustrated in a Smith Chart). A good example of using Johnson’s laws and equations over that of wave theory is the radiation pattern of a mono pole antenna when the frequency approaches a quarter (1/4) wave length (see Figure A1). As can be seen from Figure A1, the radiated intensity spikes when the length of the antenna is at ¼ wave length. This is due to the fact that the open circuit of the antenna appears as a short at the antenna input. Using wave theory, you obtain the same reflection regardless of the length where the predicted radiation is directly proportional to the length of the antenna and has nothing to do with wave length. As can be seen by the analysis below, not only are the wave theory equations more difficult to use than those formulated by Kirchoff, but they also have strict boundary conditions. These are:
Wave theory will provide accurate results to a circuit problem, but only when the above constraints are met. Consider the following illustration: Given Circuit: Let ZL and ZS equal the following: a) ZS = 50 Ω, ZL = 50 Ω b) ZS = 50 Ω, ZL = 1 Ω c) ZS = 50 Ω, ZL = 2500 Ω d) ZS = 50 Ω, ZL = 1 + j49.99 Ω e) ZS = 1 – j49.99 Ω, ZL = 1 + j49.99 Ω Using circuit theory: a) ZS & ZL = 50 Ω, I = 1.0 Amps b) ZS = 50 Ω, ZL = 1 Ω, I = 1.9608 Amps c) ZS = 50 Ω, ZL = 2500 Ω, I = 0.0392 Amps d) ZS = 50 Ω, ZL = 1 + j49.99 Ω, I = 1.4105 Amps e) ZS = 1 – j49.99 Ω, ZL = 1 + j49.99 Ω, I = 50.0 Amps Using wave theory: Reflected Loss (RL) = (K+1)2 / 4(K) where K = Zo / ZLoad a) ZS & ZL = 50 Ω, RL = (1+1)2 / 4(1) = 1.0 b) ZS = 50 Ω, ZL = 1 Ω, RL = (50+1)2 / 4(50) = 13.005 c) ZS = 50 Ω, ZL = 2500 Ω, RL = (.02+1)2 / 4(.02) = 13.005 d) ZS = 50 Ω, ZL = 1 + j49.99 Ω, RL = (1+1)2 / 4(1) = 1.0 e) ZS = 1 – j49.99 Ω, ZL = 1 + j49.99 Ω, RL = (1+1)2 / 4(1) = 1.0 The reflective coefficient (RC) is as follows: a) ZS & ZL = 50 Ω, RC = 0 or 0% Reflected b) ZS = 50 Ω, ZL = 1 Ω, RC = .923106 or 92.3106% Reflected c) ZS = 50 Ω, ZL = 2500 Ω, RC = .923106 or 92.3106% Reflected d) ZS = 50 Ω, ZL = 1 + j49.99 Ω, RC = 0 or 0% Reflected e) ZS = 1 – j49.99 Ω, ZL = 1 + j49.99 Ω, RC = 0 or 0% Reflected When: a) ZS & ZL = 50 Ω b) ZS = 50 Ω, ZL = 1 + j49.99 Ω c) ZS = 1 – j49.99 Ω, ZL = 1 + j49.99 Ω The reflected power is zero (0) d) ZS = 50 Ω, ZL = 1 Ω e) ZS = 50 Ω, ZL = 2500 Ω The reflected power is: (.923106) (50) = 46.1553 watts Therefore the power absorbed by the load impedances when ZS = 50 Ω and 50 – 46.1553 = 3.8447 watts The current through the load impedance using wave theory is: a) ZS & ZL = 50 Ω, I = 1.0 Amps b) ZS = 50 Ω, ZL = 1 + j49.99 Ω, I = 1.0 Amps c) ZS = 1 – j49.99 Ω, ZL = 1 + j49.99 Ω, I = 1.0 Amps d) ZS = 50 Ω, ZL = 1 Ω, I2(1.0) = 3.8447 I = 1.9608 Amps e) ZS = 50 Ω, ZL = 2500 Ω I2 =3.8447/2500 I = 0.0392 Amps Therefore:
Based on the above arguments, Figure A1, and the results of the above illustration, it can be concluded that “wave theory” is only a theory. |
 George M. Kunkel is the founder and chief engineer of Spira Manufacturing Corporation. He holds both B.S & M.S. degrees in Engineering from UCLA, and has been active with the IEEE EMC Society for 50 years, serving as a chairman of multiple technical committees and working groups. Kunkel has authored over 100 EMC technical papers and revised several SAE-ARP test standards. He can be reached at George@spira-emi.com.
George M. Kunkel is the founder and chief engineer of Spira Manufacturing Corporation. He holds both B.S & M.S. degrees in Engineering from UCLA, and has been active with the IEEE EMC Society for 50 years, serving as a chairman of multiple technical committees and working groups. Kunkel has authored over 100 EMC technical papers and revised several SAE-ARP test standards. He can be reached at George@spira-emi.com.